09. Ensemble methods - Boosting: AdaBoost

9주차. Ensemble methods - Boosting: AdaBoost

 

서울시립대학교 인공지능학과 노영민 교수님의 데이터 마이닝 강의를 정리함을 미리 알립니다.

 

 

• Boosting: AdaBoost

우리는 계속 복잡한 Strong model을 사용하여 문제를 해결했다. 하지만 Random Forest와 같은 Weak model들을 여러개 사용하여 문제를 해결하는 방법도 존재했다... 그러한 모델 중 우리는 AdaBoost를 공부할 것이다.

cf) 여기서 Weak model은 랜덤 추측보다 조금 더 나은 정도의 성능을 보여주는 모델이다. 

AdaBoost 학습 과정

AbaBoost는 각 라운드를 거치며 순차적(,sequentially)으로 학습이 진행되며 각 라운드마다 새로운 Weak model이 존재한다. 각 라운드의 마지막에서 잘못 분류된 샘플에 더 높은 가중치를 부여하여 다음 라운드의 Weak 모델이 해당 샘플을 더 잘 학습할 수 있도록 한다. 학습이 끝나면 이후 각 모델에 가중치를 주고 결과들을 합쳐 예측을 진행한다.

 

쉽게 말하면 한 사람이 수학 문제집을 풀고, 틀린 것을 집중해서 체크해주면 그걸 다음 사람이 푸는.. 그리고 마지막에 모든 사람들이 모여서 수학 문제를 해결하는 느낌이다. 아래는 이에 대한 예시이다.

Round1. 하나의 weak tree로 분류를 할 것이다.

아무 weak tree나 사용하면 안된다. weak 모델이지만 가장 좋은 분할 포인트를 가져야한다.(Gini index, IG 등.. 이용)

Round1

하나의 weak 모델로 분류를 하고, round의 마지막에 틀린 데이터를 강조했다.

Round 2

다음 라운드로 오면 새로운 Weak model이 있을 것이다. 새로운 Weak model의 최적 분할 포인트를 찾아 분류하고 틀린 걸 강조했다. 이 때 중요한건 Round2의 Weak model은 전 라운드에서 강조된 문제를 맞추려고 할 것이다.

Round 3

이러한 과정을 정해놓은 hyperparameter까지 계속 반복한다. 그러면 각 라운드의 모델 에러와 가중치가 나오게 된다.

3개의 weak model을 사용한다고 미리 설정해놨다고 해보자. 그러면 이렇게 모델이 완성된다. 이제 새로운 데이터에 대한 일반화 과정을 간단하게 그림으로 보이겠다.

새로운 데이터에 대한 예측

각 라운드의 모델들의 정답과 가중치를 고려하여 새로운 데이터에 대해 예측을 진행했다. Test data 점을 확인하라.

앙상블 식

 

이러한 AdaBoost의 알고리즘은 다음과 같다. 

알고리즘 의사코드 암기 해놓자.

 

 

<Example> ***

문제를 풀면서 알고리즘을 이해해보자. S의 요소인 $D_1$은 균등 분포를 따르므로 모든 확률이 같을 것이다.

(Round 1)

D1이 균등 분포를 따른다.

여기서 가장 좋은 weak model을 찾아 분류하고, 그 모델의 에러를 찾아 0.5가 넘는지 확인한다. 넘지 않는다면 해당 모델의 가중치를 계산하고 다음 모델에서 사용될 데이터의 가중치$D_{i+1}$를 계산한다. 모델 가중치를 계산하는 식과 다음 모델에서 사용될 데이터의 가중치를 계산하는 식은 꼭 외워놓아야 한다.

Round1에서 사용할만한 weak model들..

손으로 모든 모델을 다 구할 수는 없으므로 간단하게 3개의 weak model 후보가 있다고 해보자. 우리는 각 모델들 중에 어떤 모델이 가장 좋은 모델인지 확인해야 한다. 이 때 사용하는게 바로 가중 평균 Gini index이다.

5. Decision Tree에서 설명한 적이 있다.

이건 Gini Gain에 대한 설명이다. 기존의 Gini-index와 나눈 후의 Gini-index의 차이를 보면 된다. 이 때 나뉜 데이터의 스케일을 고려해야한다.&G_L G_R&을 확인하면 빼기 전에 데이터의 스케일 (나뉜 갯수/ 나뉘기 전 갯수)로 조정을 해준다. 

 

  AdaBoost에서 사용되는 약한 학습기가 결정 트리일 경우 가중 평균 Gini index가 가장 작은 걸 사용한다. ***

Gini Gain을 얻기 위해 기존의 Gini index에서 뺀 값이 바로 가중 Gini index이다...

Chast pain을 기준으로 Yes 집단과 NO 집단으로 나눴을 때의 가중 평균 Gini index

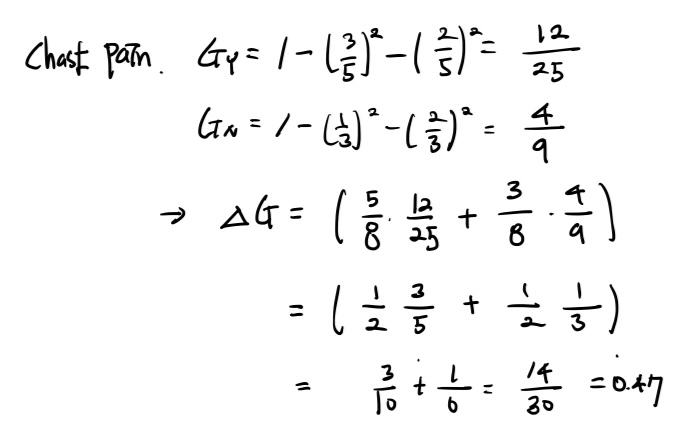
이 계산을 모든 후보에 적용하면 된다.

Round 1의 Weak model이 결정 되었다.

알고리즘에 따라 에러를 계산하고, 모델의 가중치를 계산하고, 다음 라운드에서 사용될 데이터의 분포를 결정한다.

No 집단에 Y가 1명 있으므로 전체 에러는 1/8

if 문을 통과하여 이제 해당 모델의 가중치를 계산할 것이다.

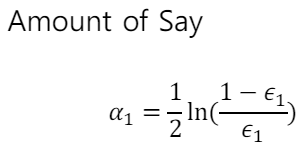
위 모델 가중치을 토대로 다음 Round의 데이터 분포를 결정할 가중치를 계산한다.

다음 라운드의 데이터 가중치를 계산하므로써 틀린 문제가 강조된다. $y_i$와 예측값인 $ h_t(x_i) $ 가 1과 -1의 값을 가진다고 해보자(분류 문제니까..) 만약 실제 값 $y_i$와 $ h_t(x_i) $ 가 같다면 알파는 양수이므로 해당 i열의 데이터 포인트의 가중치는 감소할 것이다. 이와 반대로 다르다면 증가할 것이다. 

다음 Round의 데이터 가중치를 계산하고 있다.

틀린 4번 째 열의 데이터 포인트는 가중치가 증가하였고, 맞은 나머지 열들의 가중치는 감소한다.

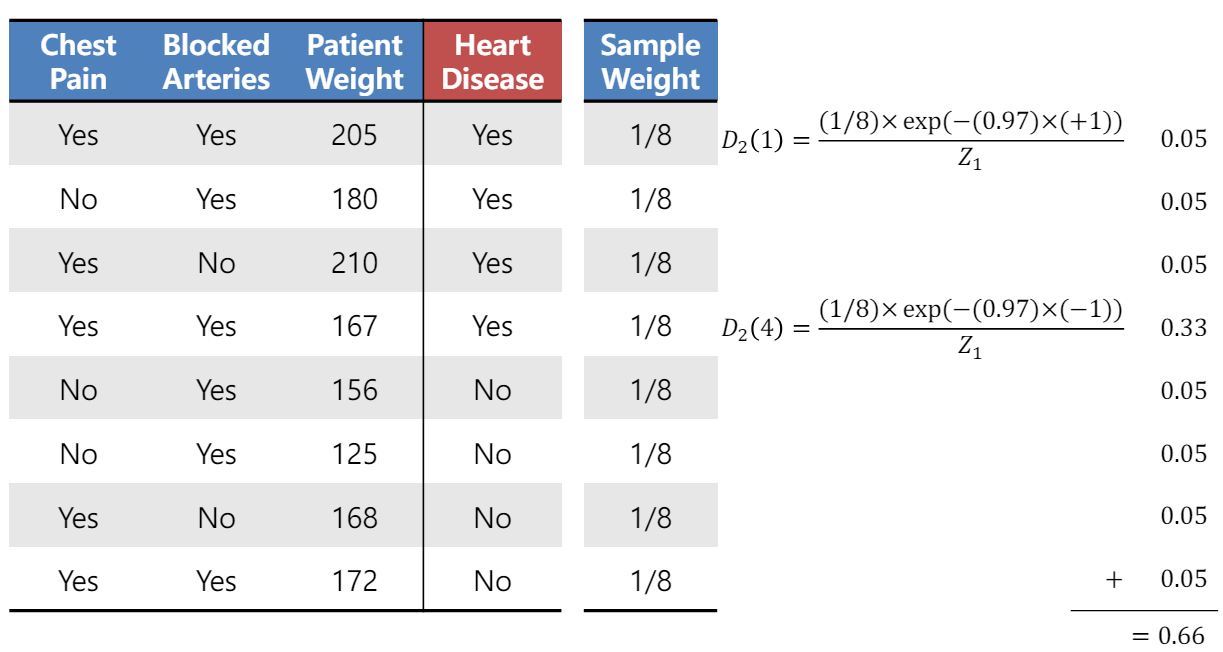
여기서 정규화 요소인 $Z_t$를 빼먹으면 안된다. vaild한 분포가 되기 위함이다.  $Z_t$는 정규화 전의 모든 가중치를 더하면 된다.

0~1 난수를 발생시켜 데이터를 샘플링한다.

다음 라운드에서 사용될 데이터 가중치가 계산되었다. 이 가중치를 토대로 데이터를 뽑으면 틀린 데이터 포인트를 더 많이 뽑을 것이다.(복원 추출) 

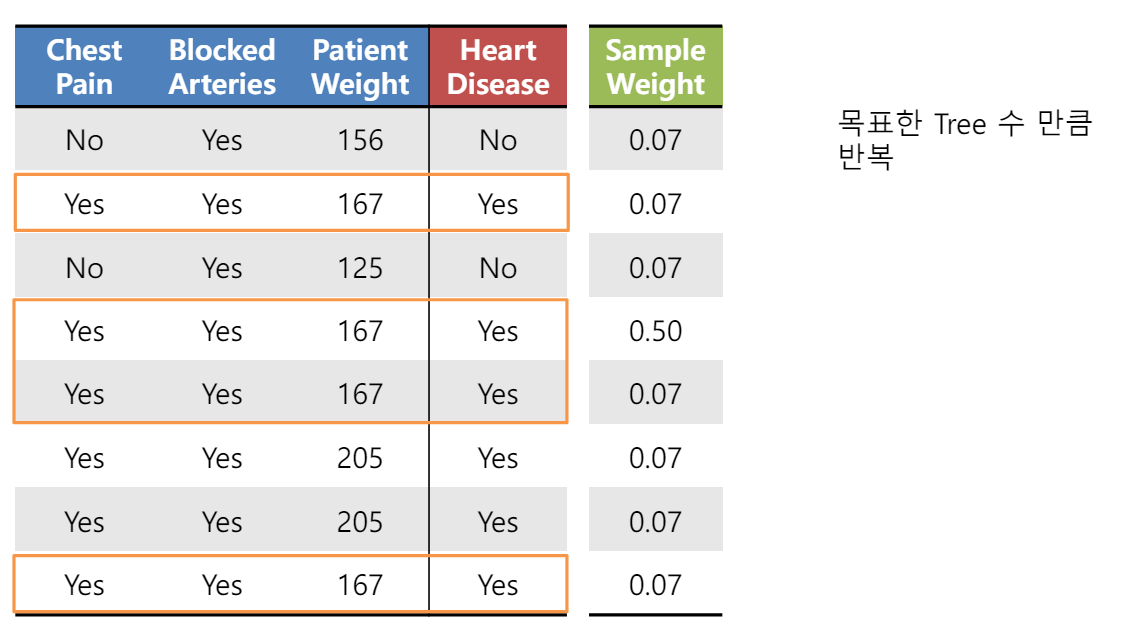
이렇게 하면 한 라운드가 끝이 난다. Round2에서는 이렇게 틀린 분류가 강조된 데이터를 갖고 학습을 진행할 것이다. 이제 이 과정을 정해놓은 hyperparameter T에 대해 반복하면 된다.

 

아래는 데이터들이 분류되고, 강조됨을 반복하며 학습됨을 보인다.

 

 

 

• Bagging vs. Boosting ***

https://dogunkim.tistory.com/16

6. Random Forest

위 글에서 Bagging에 대해 설명해놨다. 

 

Bagging은 복원 추출을 통해 데이터셋을 구성하고 그렇기에 학습을 병렬적(Parallel)으로 할 수 있다. 하지만 Boosting은 병렬적인 학습이 불가능하다. 병렬적인 학습이 불가능하기에 Boosting는 다소 학습이 느릴 수 있다.

 

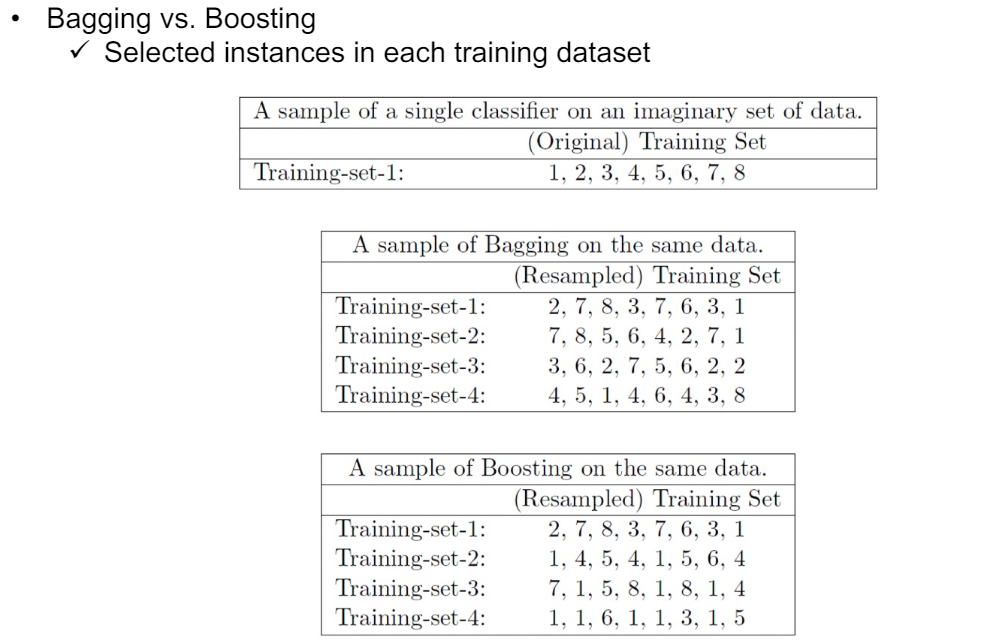
Bagging은 복원 추출하기에 sample을 뽑을 때 서로 영향을 주지 않는다. 하지만 Boosting의 경우 제대로 분류하지 못한 어려운 샘플을 더 많이 뽑으므로 sample을 뽑을 때 서로 영향을 준다. 즉 독립적이지 못하다. 위 예시를 보면 Bagging의 경우 data point 1이 많이 뽑히고 있는 걸 볼 수 있다. data point 1가 분류를 제대로 하지 못한 data point일 것이다.

 

정리. Bagging vs. Boosting ***시험 대비

차이점 1.

Bagging은 병렬적 학습이 가능, 하지만 Boosting은 병렬적 학습이 불가능하고 순차적인 학습을 하며 학습 속도가 느림.

 

차이점2.  

Bagging은 샘플링이 독립적임. 하지만 Boosting은 제대로 분류하지 못한 샘플에 더 큰 가중치를 주기에 샘플링이 독립적이지 않음.