8. Support Vector Machine with Soft Margin

8주차. Support Vector Machine with soft margin

 

서울시립대학교 인공지능학과 노영민 교수님의 데이터 마이닝 강의를 정리함을 미리 알립니다.

 

• Linearly Non-separable Problem

만약 데이터가 초평면으로 완벽하게 구분되지 않는다고 해보자. 이를 (Linearly nonseparable)라고 한다.

이런 데이터의 경우 hard margin을 갖는 SVM을 적용하면 제약식을 만족할 수 없다는 문제가 생긴다.

기존의 SVM 모델. train data를 완벽하게 separating하지 못하므로 제약식을 만족할 수 없다. 즉 해가 존재하지 않다.

 

이렇게 Linearly nonseparable일 때 다음과 같은 전략을 취할 수 있다.

 

1) 예외를 허용한다.

2) 넘어가는 정도를 Penelty로 정의한다.

3) Margin을 최대화함과 동시에 Penelty를 최소화한다.

plus/ minus plane을 넘어가도 분류할 수 있도록 기존 제약식 우변에 패널티를 준다.

이런 전략으로 train error를 허용하는 Soft margin Support vector machine를 만들어보자.

 

 

• Soft margin Support vector machine

Margin을 최대화함과 동시에 Penelty를 최소화하는 Optimal Problem은 다음과 같을 것이다.

Soft margin Support vector machine

뒤에서 C에 대해 다시 언급할 것이다. C는 tuning parameter로, 패털티의 총합을 조절한다. 패털티 총합의 계수 C가 크면, 패널티는 작을 것이다. (목적함수의 Min을 보면서 C를 키워보면 바로 이해할 수 있다. 즉 패널티를 억제하는 역할을 한다.)

 

 

• Lagrange Dual formulation

기존 Optimal problem을 풀기 위해 라그랑즈 승수법을 이용한다.

ch7에서 LP를 만드는 방법을 설명했다.

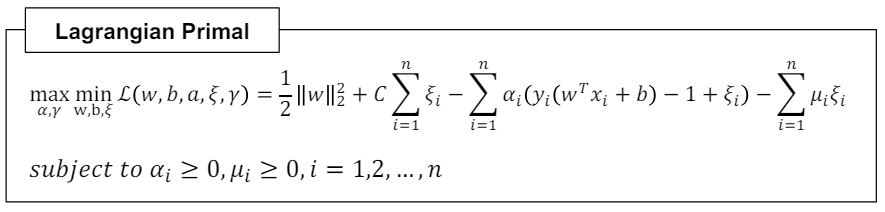
임계점 정보를 사용하여 Lagrangian Dual Formulation를 만든다.

목적함수는 변하지 않았다..

엄밀하진 않지만, 풀이를 첨부하겠다.

시험 대비

 

구한 해가 Lagrangian dual problem의 해가 되기 위한 조건은 다음과 같다. (KKT condition)

KKT 암기..

여기서 주목할 것은 Complementary slackness이다. 기존의 hard margin SVM은 알파 값에 따라 S.V인지 아닌지 결정할 수 있었다. soft margin의 경우도 마찬가지이다. 라그랑즈 듀얼의 제약식에서의  $ 0 <= α_i <= C $ 조건을 기억하자.

 

알파에 따라 3가지 KKT 조건을 이용하여 S.V를 구분하는 과정.

 

 

• Impact of C

기존의 목적함수에서 C가 크면 패널티가 커지지 못했다. 즉 C와 패털티는 반비례한다. 

예상 문제.. C가 크면 패널티가 작아(허용 많이 x) margin이 좁다..

C가 매우 커지면, hard margin과 거의 같아진다..