서울시립대학교 인공지능학과 노영민 교수님의 데이터 마이닝 강의를 정리함을 미리 알립니다.
5. Decision Tree (,의사결정나무)
- Decision Tree
의사 결정 나무란 데이터에 내제되어 있는 패턴을 변수의 조합으로 나타내는 예측/ 분류 모델을 Tree의 형태로 만든 것이다.

Decision의 쉬운 예시

Decision 개요
input data에 따라 분류를 하는 Decision Tree와 예측을 하는 Decision Tree가 있다.
우리는 Decision Tree를 만들기 위해 한 feature를 선택하고 데이터를 분할한다. 이때 데이터가 균일하도록 분할해야한다. 여기서 데이터가 균일하다는 것은. 불순도(impunity)가 낮거나, 분산이 작은 걸 의미한다. 이에 대해서는 뒤에서 다룬다.


한 feature를 선택하고, 데이터를 쪼갠다... 결정 tree를 그려 나가며 정확도를 높혀간다.
- Regression Tree ,회귀를 위한 결정 트리
왼쪽은 Regression Tree이고, 오른쪽은 Logistic regression을 통한 모델이다. 물론 Tree로 표현한 건 아니다.

회귀 트리의 Decision boundary는 축과 수직/수평 한데, 그 이유는 결정 트리는 데이터를 분할 할 때, 한 개의 feature를 이용하기 때문이다.

이러한 결정 트리 모델이 만들어졌다고 하자.
만약 여기에 새로운 값이 결정된다면, 해당 class의 평균값으로 정해진다. 다음과 같은 식으로 표현할 수 있다.


위 회귀 트리의 리프노드가 5개로 나뉘므로 시그마는 5까지 더한다.
만약, 새 데이터가 R3로 분류된다고 해보자. 시그마를 모두 더하면, C3항만 살아 남을 것이다. 그러므로 새 데이터의 예측값은 R3의 평균값으로 반환될 것이다.
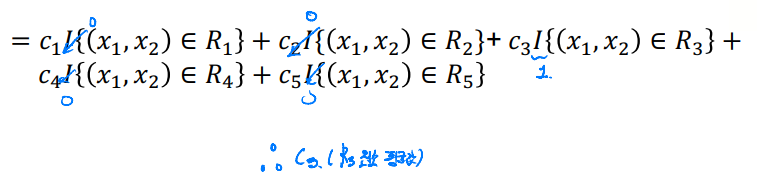

새로운 데이터가 3 값을 갖는다고 예측했다.
이를 일반화 하면 다음과 같다.

새 데이터가 Rm에 속할 때, 그 Rm의 평균값을 예측값으로 내놓는다.
# 우리는 그러면 어떻게 하면 최상의 상태로 분할할까? 를 고민해야한다. (Regression Tree의 경우)
- Regression Tree 최적 분할 방법
# 분산을 작게 분류해라. (불순도(Impurity)를 측정하는 SSE를 최소로 하라)
아까 초반에 데이터의 한 feature를 잡아 분할할 때, 데이터가 최대한 균일하게 분할해야한다고 말했다. 즉 갈라진 데이터가 균일해야한다는 것인데.. 이는 분산이 작음을 의미한다.
-> 회귀 모형에서 분산이 낮은 것을 pure하다고 본다. 즉 불순도를 낮게 해야한다.

불순도를 측정할 때 사용한 SSE가 Cost function이 된다. # 불순도 검사를 위해 SSE를 쓰는 것을 암기.
-> 즉 불순도를 줄이기 위해 불순도 측정하는 SSE를 Cost function로 잡고 이걸 작게 하면 된다.

실제 값과, 예측 값의 차이를 최소로.. 이건 그냥 당연한 소리..
각 분할에 속해 있는 y값들의 평균으로 예측했을 때, 오류가 최소이다.
위 ex1)를 직접 계산해보자.
cf) 분할을 위해 가장 먼저 고른 feature는 가장 중요한 feature이다.
- Classifier Tree (분류를 위한 결정 트리)

뭐 다른건 딱히.. 없다.. 연속된 값을 예측하느냐, 클래스를 예측하느냐.. 이정도...
새로운 데이터가 R5에 결정 트리를 통해 분류되어 R5에 속한다고 생각하자. 이 예측값을 구하는 건 다음과 같다.

이 함수는 이어서 설명한다.
k(m)는 마지막 leaf node m(Rm)에서 가장 높은 관측 비율을 보이는 클래스를 반환한다. 이를 자세히 설명하면 다음과 같다.

argmax는 최대 값을 갖는 클래스 k를 배출하는 함수이다. 예시를 잘 봐라.
예시를 잘 보자. 분류 끝에 leaf node(맨 끝 노드) 1번에 class 1, 2, 3 ,4가 저렇게 있다고 생각하자. 우리는 각 class 의 관측 비율을 계산하고, 관측치가 가장 높은 클래스로 결과값을 내놓을 것이다. 만약 새로운 데이터가 들어와 분류 끝에 예시인 R1로 들어오면 그 데이터는 class 4로 분류될 것이다.
- classifier tree 분할 방법 ******
음.. regression tree(회귀 트리)에서는 불순도을 계산하는 SSE를 Cost function으로 잡고 이를 최소로 하여 최상의 분할을 찾았다... (모르겠으면 위에 다시 읽어라...)
classifier tree에서는 최상의 분할을 찾는 방법이 조금 다르다. entropy(혼잡도)의 개념이 들어오고, impurity(불순도)를 계산하는 방법도 회귀 트리와 다르다.ㅁㅁ

- Impurity(불순도) 측정

cf) 불순도가 높을 수록, 정보가 많다는 뜻이다. (여러 가지가 있을 거니까..)
이를 측정하는 방법은 3가지가 있다. (3가지 방법 암기)

한 leaf node (m)를 잡고 계산을 진행하는 거다.

(^pk는 해당 leaf node m에 대한 각 클래스의 관측치 비율이다.)

m = 1일 때의 예시
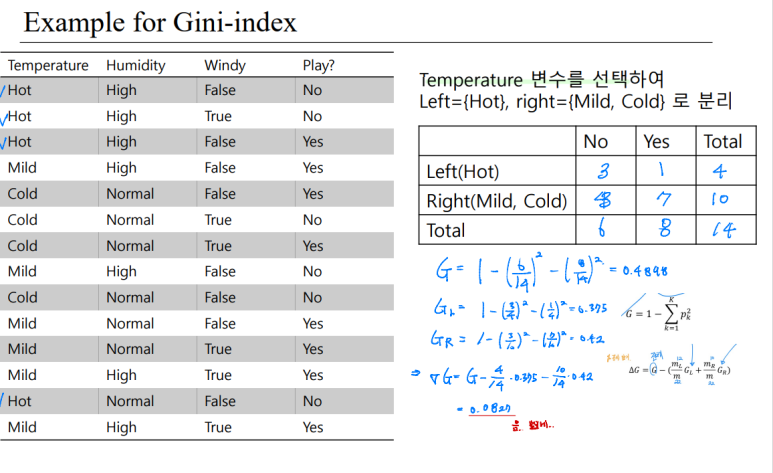
위 leaf node에서 k = 4이고(관측치 비율이 가장 높은 class) Misclassification rate는 1 - 4/7 = 3/7이다.
gini index는 관측치가 높은 class에만 계산하는 것이 아닌 시그마를 통해 모든 class를 계산에 사용한다.
gini index = 1 - (1/7)^2 - (1/7)^2 - (1/7)^2 - (4/7)^2
3가지 방법 모두, 불순도가 최대일 때 최대이고, 불순도가 최소(0)일 때 최소이다. 즉 우리는 이 3개의 방법 중 어떤 걸 쓰던지.. 이걸 최소로 만들면 불순도가 낮아 최적의 분류가 되는 것이다.
# Entropy의 계산. (불순도 계산 3번) ******
1, 2, 3 leaf node가 있다고 생각해보자. 이에 대한 entropy 계산은 다음과 같다.

얘도 모든 class를 계산에 이용한다.
이건 각 끝 노드에 대한 entropy 계산이다. 이걸 활용하는 방법은 다음과 같다.
- Information Gain (줄어든 entropy의 양)

나눠진 모든 노드의 entropy를 구한다. 구한 각각의 entropy를 노드 사이즈/ 분할 전 노드 사이즈로 곱하고 이를 전 노드의 entropy에서 뺀다.
# 크기 비율을 곱하는 이유는 다음 노드에 1개만 보냈을 때, entropy가 0이 나오므로.. 유리하기 때문이다.

해당 예시에서 Information Gain 값은 다음과 같다.
1 - ( 3/7 * 0.5 + 4/7 * 0.5 ). 이게 바로 줄어든 entropy의 양이다. 우린 이걸 최대로 해야한다.
# 다른 값과 다르게 Information Gain은 최대로 해야한다. 줄어든 entropy의 양이니까..

IG를 구해서 별로 entropy가 안줄었으므로.. 이렇게 나누지 말자! 라는 결론이 나온다.
# Gini-index 도 이렇게 원래꺼 - 크기보정값 수치를 구할 수 있다. 이를 최대로 하면 된다. ******
이러한 방식을 통해 Gini-index 또한 얼마나 줄어들었는지 확인할 수 있다. 이 또한 이걸 최대로 하면 된다.
# 애도 크기 비율을 꼭 곱해서 빼줘야한다.

각 노드의 gini-index 공식은 위에서 배웠다. 갈라진 노드의 각 gini-index를 구하고 합쳐서, 원래 노드의 gini-index에서 뺀다. # 크기 보정은 필수다.

- 정리, 결정 트리 단점
우리는 좋은 예측을 하는 Decision Tree를 만들기 위해 (분류 결정 나무인 경우) 순도가 높게(불순도가 낮게),
혹은 (회귀 결정 나무의 경우) 분산이 낮게 데이터를 나누고 싶다. 이를 위한 수치는 다음과 같았다.
우선 '회귀(Regression)' 하는 결정 트리의 경우.. SSE를 보았다. 이걸 최소로 하면 분산이 낮은 최적의 분할을 할 수 있었다.

'분류(Classifier)' 결정 트리에서 좋은 분할을 하기 위해 Impurity를 보여주는 수치는 총 3개였다.

한 leaf node (m)를 잡고 계산을 진행하는 거다.
우리는 이 3개를 최대한 낮추고 싶다. (비슷한 범주 끼리 묶고 싶으니까) 각 계산 방법을 꼭 숙지해야한다.


또한 우리는 얼마나 좋아졌는지를 계산할 수도 있다.이 때 쓰는 것이 IG와 G -각 노드의 gini-index이다. (Impurity Gain)이라고 한다.. 이건 나아진 정도를 말하므로, 최대한 높히고 싶은 수치이다.
# 계산할 때 꼭 크기 보정이 필요하다. (1개만 보내면 너무 너무 유리하니까)
# 결정 트리의 단점 (4개)
결정 트리는 계층적 구조로, 중간에 에러가 생기면 이 에러가 다음 단계로 전파된다. 학습 데이터의 미세한 변동에도 최종 결과가 크게 영향을 받고, 적은 개수의 노이즈에도 크게 영향을 받는다. 또한 최종 노드의 갯수를 늘리면 과적합의 위험이 생긴다.
(그니까 나무가 연약하다.. 나무 양잿물 한 번 주면.. 날씨 좀 안좋으면.. 중간에 끊어버리면... 너무 커져버리면...)

과적합(overfitting)
이를 해결하기 위해 Random forest을 사용한다.
'학부 수업 > 데이터마이닝' 카테고리의 다른 글
| 7. Support Vector Machine with hard-margin (2) | 2024.06.17 |
|---|---|
| 6. Random Forest (3) | 2024.05.20 |
| 4. Linear Models (1) | 2024.05.20 |
| 3. K-Nearest Neighbors (KNN) (1) | 2024.05.20 |
| 2. Supervised Learning(지도 학습) (0) | 2024.05.20 |