(서울시립대학교 인공지능학과 노영민 교수님의 데이터 마이닝 강의를 정리함을 미리 알립니다.)
3주차. K-Nearest Neighbors
# Model-Based vs. Instance-Based Learning

Model-Based Learning(모델 기반 학습): 학습 데이터를 활용해 모델을 구축(학습 단계), 모델을 사용하여 예측.
Instance-Based Learning(사례 기반 학습): 학습 단계에서 하이퍼파레미터를 결정한 후, 새로운 인스턴스를 학습 데이터와 비교하여 예측한다. (갖고 있는 걸 새로운 것과 비교 대조 하는 느낌이다..)
약간 공부를 잘 해놓은 친구 vs 공부는 잘 안했지만 족보를 잘 들고 있는 친구 느낌이다.
인스턴스 기반 학습은 훈련 시간이 덜 걸리지만(하이퍼파라미터만 결정), 예측 시간이 소요가 많이 된다. 시간이 지남에 따라 훈련 데이터가 점진적으로 제공될 때 유리하다.
(Instance-based learning takes less time in training but more time in predicting, and is advantageous when training data becomes available gradually over time.)
# k-Nearest Neighbors (인스턴스 기반 학습의 종류)
가장 가까운 K개의 데이터 포인트를 통해 새로운 데이터 포인트를 예측(분류(classification), 혹은 회귀(regression))한다.
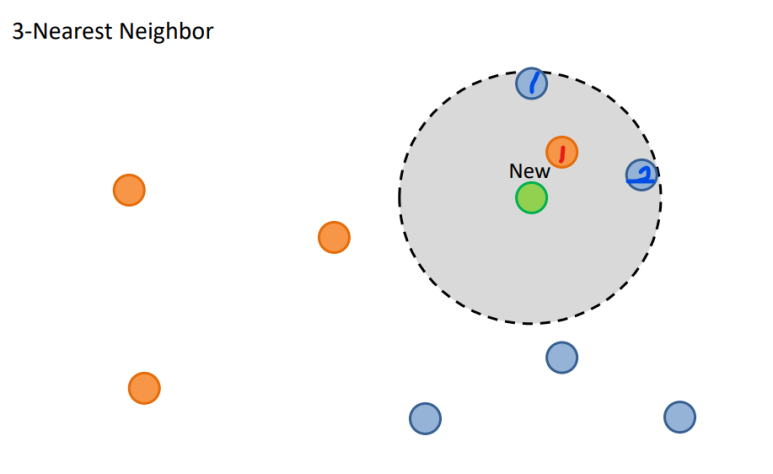
K = 3, 가장 근접한 3개의 이웃 데이터 포인트 중 파랑이 2개, 주황이 1개 이므로 새로운 데이터 포인트는 파란색으로 예측(분류)될 것이다. (Classification 그림 예시)

(Classification 예시)
위 테이블에서 만약 K = 1인 1-Nearest Neighbors를 한다면, 가장 가까운 거리의 1행 데이터 포인트로 예측하여, Class1로 분류될 것이다. (K=3이여도 마찬가지.. 1, 1, 2..)
# k-Nearest Neighbors; Compare to Linear model

음 그렇군..
# k-Nearest Neighbors - 1) Classification

다음 표를 k-Nearest Neighbors - Classification 할 것이다.
다음과 같은 분류 알고리즘을 사용한다.
- 분류할 관측치 x를 선택(새로운 데이터 포인트.. G)
- x로 부터 인접한 k개의 학습 데이터를 탐색(k는 하이퍼파라메터로 학습 과정에서 유저가 설정)
- 탐색된 k개의 학습 데이터의 majority class c를 정의(걍 어떤 class가 가장 많은지 확인)
- c를 x의 분류 결과로 반환

k = 1일때의 majority class와 k = 3일때의 majority class가 다르다.
# k-Nearest Neighbors - 2) Regression

G 데이터 포인트에 대한 Regression
다음과 같은 예측 알고리즘을 이용한다.
1. 예측할 관찰치 x를 선택(예측할 새로운 데이터 포인트)
2. X로부터 인접한 k개의 학습 데이터를 탐색
3. 탐색된 k개 학습 데이터의 평균을 x의 예측 값으로 반환(Classification과 달리 평균값이 반환된다.)

결과
k에 따라 예측 결과가 달라진다. 즉 우리는 hyperparameter인 k를 더 효과적이게 설정해야 한다...
# k-Nearest Neighbors - hyperparameters
무엇이 효과적인 k이고, 거리 측정 법 선택(Distance Metric selection)을 배울 것이다.
1. Which k is most effective

k에 따라 결과가 달라진다.. 우리는 이 k가 어떨 때 효과적인지 알아야한다.
cf) k-Nearest Neighbors는 Instance based learning이라, decision boundary가 그려지지 않는다.
하지만, 위 그림처럼 데이터 포인트가 들어올 수 있는 모든 위치(격자점)에 k-Nearest Neighbors를 돌리면 decision boundary를 그릴 수 있다.
다음과 같은 수치를 통해 k를 선택할 수 있다.
-> Classification의 경우 MisClassError 수치를 이용한다.

함수 I는 예측값과 실제 값이 틀릴 때, 1를 output으로 맞는 경우 0을 output으로 내보낸다.
-> regression의 경우 SSE(Error sum of squares) 수치를 이용한다.

예측값과 실제값의 차이의 제곱.. (부호 떄문에 제곱을 해준다.)
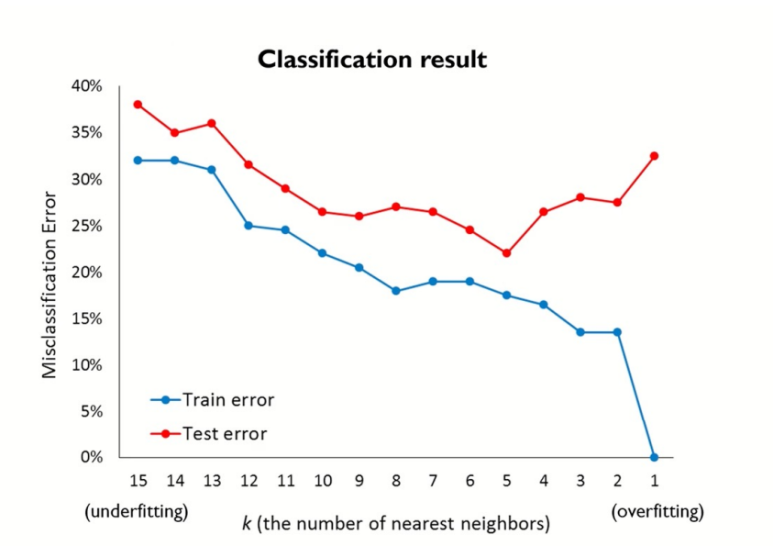
분류.. k=5쯤에 Test Error가 가장 적으므로.. k=5쯤이 적당해 보인다.
2. Distance Metric selection(거리 측정법 선택)
1) Euclidean Distance
2) Minkowski distance: Euclidean distance 의 일반화된 형태
3) Manhattan Distance (L1-distance)
4) Mahalanobis Distance
5) Correlation Distance
# Weight를 사용한 K-Nearest Neighbors
k에 따라 가까운 데이터 포인트를 선택하고, 이를 통해 예측을 한다.
만약 k = 3 인 경우, 3개의 데이터 포인트의 거리가 각 1, 5, 9999 라고 생각해보자.
거리가 1, 5인 데이터 포인트들은 가깝다고 말 할 수 있지만, 거리가 9999인 데이터 포인트는 3번 째로 가깝기에 선택된 데이터 포인트일 뿐.. 새로운 데이터와 그렇게 가깝다고 말 할 수없다.
-> 그렇게에 우리는 거리를 고려해 가중치를 사용할 수 있다.

가중치를 사용한 예측과 그냥 위에서 설명한 예측 비교.. 자주 읽어보면서 수식을 이해하자.
# Hyperparameters 종류 (학습 과정에서 유저가 결정)
1) Distance metric (거리 측정 방법 선택)

2) The number of nearest neighbors k (k 선택)
Smaller k -> capture local structure in data (but also noise)
Larger k -> provide more smoothing, less noise, but may miss local structure
3) Weight function(가중치 함수 선택)

'학부 수업 > 데이터마이닝' 카테고리의 다른 글
| 6. Random Forest (3) | 2024.05.20 |
|---|---|
| 5. Decision Tree (4) | 2024.05.20 |
| 4. Linear Models (1) | 2024.05.20 |
| 2. Supervised Learning(지도 학습) (0) | 2024.05.20 |
| 1. Introduction 데이터 마이닝이란? (3) | 2024.05.20 |