(서울시립대학교 인공지능학과 노영민 교수님의 데이터 마이닝 강의를 정리함을 미리 알립니다.)
4주차. Linear Models
- Linear Regression

x축 y축에 해당되는 두 변수의 선형 관계를 잘 설명하는 직선을 찾는게 Linear Regression 선형회귀이다.
회귀 분석을 위한 선형 모델의 경우, 예측 ŷ은 입력 특징(Input)의 선형 함수이다.
(For linear models for regression, the prediction ŷ is a linear function of input features.)
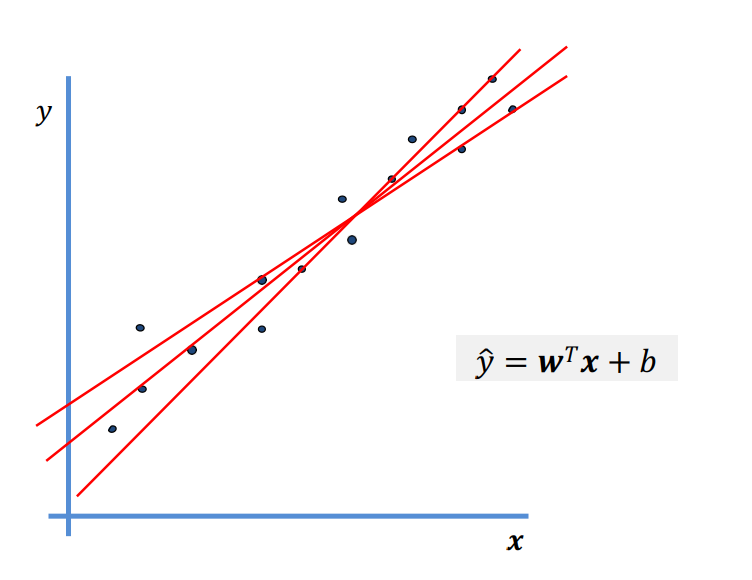
선형 회귀
cf) Relationship btw X & Y
두 변수에 대해 두 관계가 존재한다.
1) Deterministic : 확정적인 관계, X 변수만으로 Y 변수를 전부 설명한다.

2) Stochastic: 확률적인 관계, X 변수만으로 Y 변수를 전부 설명할 수 없다. 에러가 포함되어야 한다.

Stochastic.. 에러를 포함해야 X로 Y를 설명할 수 있다.
다시 한 번 말하자면, Linear Regression(선형 회귀)란 출력 변수 Y가 입력 변수 X의 선형 조합으로 표현되는 모형이다. 선형 회귀는 1) X와 Y의 관계를 숫자로 설명하고, 2) Y의 미래 가치를 예측하려는 목적을 가진다.

Linear Regression 예시 (X가 한개인 모델과, X가 여러개인 모델이 있다.)
- Categorization of Linear Regression
위에서 말했듯이, 선형 회귀는 변수가 한개인 것과, 변수가 여러개인 것이 존재한다.

변수의 갯수, 선형성에 의해 구분된다. (선형성이 없다면 선형 회귀 모델은 아니겠지..) 음 그렇군 하고 넘어가자.
- Basic of Linear Regression ***유도 후 암기***
# 오류를 정의해야한다. 내가 선형 회귀 모델을 만들었다고 해보자. (ŷ = b + ax) 여기서 예측한 ŷ 값이 실제 y 값과 다를 수 있다.(이때의 차이가 오차인 입실론이다.) 이때 x와 y는 Stochastic 관계이다.
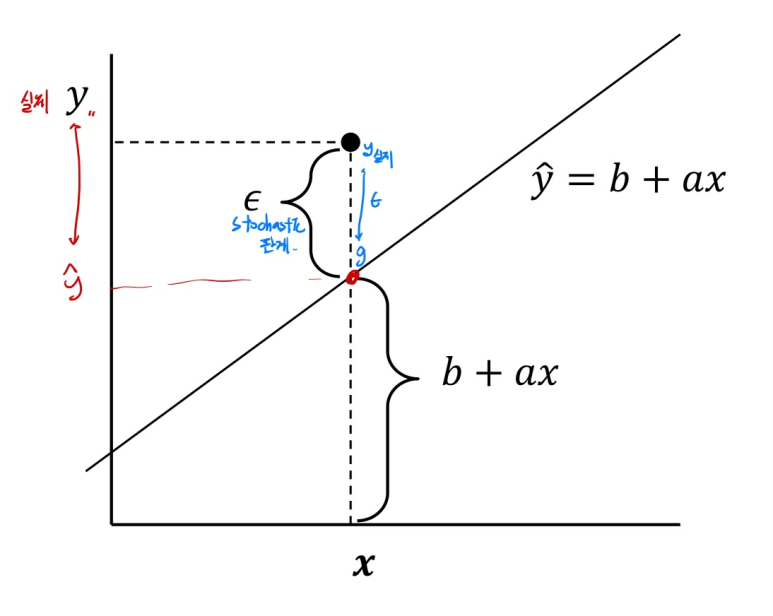
예측값 ŷ과 실제 값인 y의 차이가 생긴 경우.
우선 에러에 대한 4가지의 가정을 알아두자. 1)정규성, 2)비편향성, 3)등분산성,4) 독립성 이다. 선형 회귀 모델에서 발생되는 에러는 앞 4가지의 가정을 무조건 만족한다고 생각해야한다.
1) 정규성: 에러가 정규 분포를 따른 다른 가정이다.
2) 비편향성: 에러가 따르는 정규 분포가 평균이 0이다.
3) 등분산성: 에러들이 갖는 분포가 다 같은 분산을 따른다는 가정이다.
4) 독립성: 각 에러들이 서로 영향을 주지 않는다는 가정이다.
발생한 모든 에러들은 가정에 의해 다음과 같은 정규 분포를 따른다.

발생한 모든 에러들의 분포(가정에 의함)
우리는 에러를 포함한 정답 y를 구하고 싶은거다. yi(실제값)에 대한 평균과 분산에 대해 구해보자.

구하는 것.. 에러가 확정 값이 아니라 정규 분포를 따르므로..
yi에 대한 평균과 분산을 구해보자.

기대값은 선형성에 의해 쉽게 구해진다. Ei의 평균은 가정 2) 비편향성에 의해 0이다.
분산은 Var(b + axi)가 0이 된다.. (이유 다시 찾기.... ㅜ)
-> 결론: 실제 값 yi에 대한 정규 분포를 알 수 있다.

그래서 결국 선형 회귀란, 입력 변수 X와 출력 변수 Y의 평균 사이의 관계를 나타내는 직선을 찾는 것이다. (Find a straight line that describes the relationship between the input variable X and the average of output variable Y) 우리는 정확한 선형 회귀 모델을 위해서 에러를 최소화하는 parameter를 찾아야 한다.

W^t 가 에러를 최소화 하는 parameter이어야 제대로된 예측을 할 수있다.
cf) 선형 회귀 정리: 선형 회귀란 두 변수의 선형 관계를 잘 설명하는 직선을 찾는것 인데, 이 때 두 변수 사이에는 에러가 존재할 수 있다.(x만으로 y를 설명할 수 없는 Stochastic 관계) -> 우리는 이 에러를 최소화 해야만 하며, 이를 최소화 하는 parameter를 찾아야 하는 것이다...다음 설명에서 이를 확인하자.
- Find parameters (에러를 최소화 하는 parameter 찾기...!!!) ***편미분 + 연립 or 행렬 *** RE RE
풀이 1) 선형 함수 꼴에서 에러가 최소가 되는 a, b 찾기.
우선 Cost Function을 정의하자.

Cost Function을 정의. a와 b 즉 parameter의 이변수 함수로 볼 수 있다.
a, b 두 변수에 의한 이변수 함수로 Cost function을 봤을 때, 이 함수는 볼록(Convex)하므로 Global optimum 값이 존재한다. 우리는 함수값이 극소+최소 값을 가질 수 있는 a, b을 찾으면 된다. 이때 이는 편미분을 사용해서 구하면 된다.


풀이 2) General form(행렬 곱 표현)에서 에러가 최소가 되는 parameter 찾기.
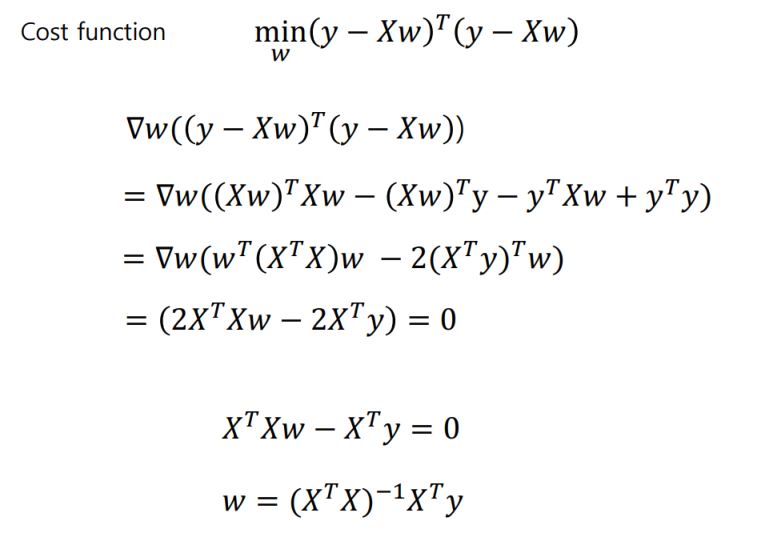
- Linear regression + regularization
우리는 선형 모델을 제한할 수 있다. 선형회귀 계수(weight)에 대한 제약 조건을 추가함으로써 모형이 과도화하게 최적화 되는 현상, 즉 과최적화를 막는다. 이를 정규화(regularization)라고 한다.

regularization 종류.. cost function 뒤에 뭘 추가해서 과최적화를 막는다.
1) Ridge regression (L2 regularization): Variance(분산)를 줄이기 위해 사용한다.

cf) Low Variance: 모델이 추론할 때, 비슷한 결과를 낸다
Low Bias: 정답에 가까운 결과를 낸다.

L2 정규화로 인해, 분산이 줄어든다.

#L2를 하는 의미.. 어떻게 분산이 줄어드는지 이해를 해야한다.
큰 parameter를 줄여서 variance를 낮추는 것이 L2 regularization의 목적이다.
parameter에 값이 골고루 배정되어야 variance가 줄어들 것이다.

L2 예시) overfitting 상황에서 잘 학습된 상황으로 바뀌기 위해서 w3, w4 매개 변수를 죽이는 작업을 했다.
위 예시에서 w3, w4를 죽이기 위한 계수 5,000은 regularization parameter라고 부른다.
이를 보통 알파로 두는데 알파가 클수록, w3, w4가 빠르게 줄어든다. (Trade off)
생각을 해봐라. w3, w4에 큰 값이 할당되면 목적함수 min은 그걸 optimal solution으로 내놓지 않겠지. ㅈㄴ 큰 수가 나올텐데.. w3, w4에 들어있는 값을 계속 줄일 것이다.

잘 생각해봐라. 어느 한 w에 너무 큰 값이 배정되면, variance가 크겠지...
뒤에 L2 를 적용하면 한 W가 크면 목적함수 min은 그걸 솔루션으로 내놓지 않고 재 조정할것이다.
l2는 모든 w에 대해 이를 적용하므로 어느 w가 튀지 않고 골고루 배정될 수 있게 돕는다.
L2 계수 알파가 클 수록 제약이 심하다. w에 더욱 작은 값들이 배정 될 것이다.
# Ridge(L2) 기하학적 설명

MSE를 전개하면 이차 곡선이 나온다.

그렇대.. 내가 생각한거 반대네..
우린 Cost function인 MSE (Mean Square Error)의 합을 최소로 해야된다. (당연하다..)
우리 모델이 타원임을 알 수 있다고 생각하자.
Ridge (l2) 정규화를 건 cost function은 다음과 한 목적함수와 한 제약식으로 나눌 수 있다.
L2의 계수 알파는 늘리면 늘릴 수록, w가 커지는걸 억제한다.

L2 식을 목적함수와 제약식으로 나눈 이 식에서의 t는 작으면 작을 수록 w가 커지는 걸 억제한다.

제약식과 접할 때, 최적의 loss와, parameter를 찾을 수 있다.
행렬로 증명하면 다음과 같다.

걍.. 음 그렇군. 식은 여러번 써보자.
2) Lasso regression (L1 regression)
# Lasso(L1)의 기하학적 증명

제약식과 접할 때.. 타원은 같은 loss를 갖는 파라메터 조합의 집합이라고 생각해라.
Loss를 포기하면서 점점 타원을 늘려간다. 제약식과 접할 때, 같은 loss 중 t가 가장 적은 점이 있다.
그림에서 w1 변수가 먼저 사라졌는데, 이는 w2보다 중요도가 떨어진다는 의미이다. 사라진건 다시 생기지 않는다.
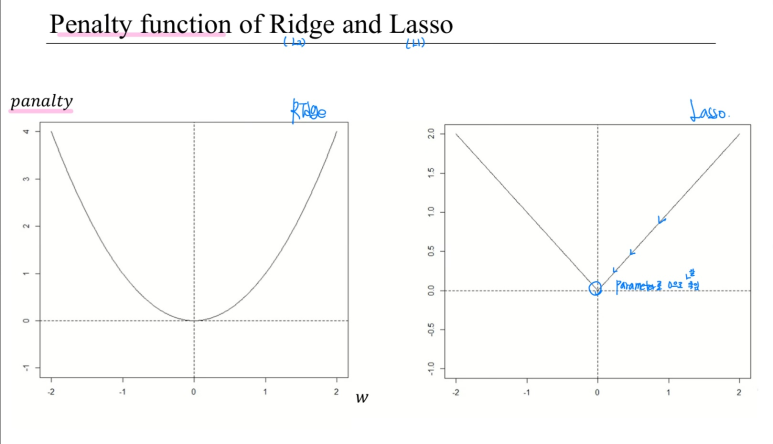
L2, L1의 각각의 패널티를 잘 생각해봐라. L2는 이차, L1은 1차 함수였다. 선형인 L1이 더 parameter를 0으로 잘 보낸다. L2는 w가 적당히 작아지면 패널티가 적당히 작다. 하지만, L1은 아니다.. 그래프를 겹쳐놓고 같은 지점을 보면 알 수 있다. # L1이 L2보다 Parameter를 0으로 더 잘 보낸다.

보라색이 Lasso의 penalty 함수이다.
같은 parameter 값을 갖더라도, L1(LASSO)의 경우가 더 패널티가 높다. L1을 적용한 모델에서는 L2를 적용한 모델보다 상대적으로 w를 더 낮추려고 할 것이다.
다음 예시를 보면 다시 한번 이를 알 수 있다.

t는 줄어들 수록 제약이 강한 거다. 제약이 강해질 수록, L1(LASSO)는 0으로 사라지는 Parameter들이 계속 보이지만, L2(Ridge)는 생각보다 잘 없어지지 않는다.
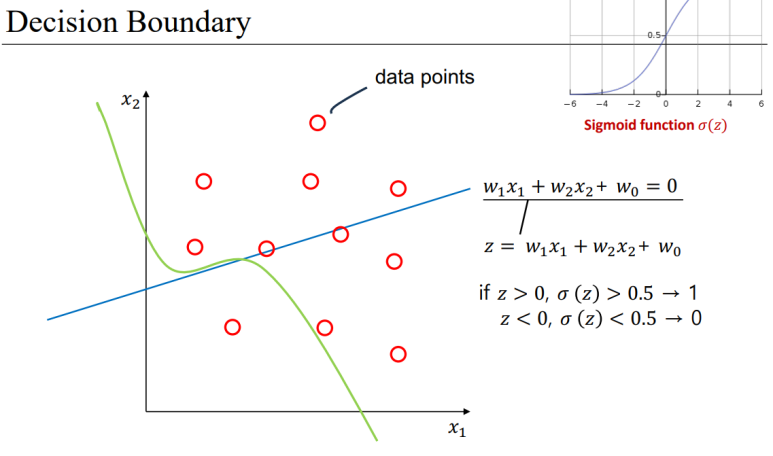
- Logistic regression

선형 회귀의 결과를 0과 1 사이로 구겨 넣는 느낌
sigmoid 함수에 나온 값을 대입하여 이를 얻을 수 있다.

이를 통해 (0, 1)로 맵핑한다.
이를 꼭 읽어보자.
Logistic 회귀에서 우리는 죄적의 parameter 를 착기 위해, "Binary cross-entropy" Loss를 사용한다.

아마 convex를 위해서 쓰지 않을까..?
위 cost function을 잘 보자. yi가 1인 경우 ^yi을 1로 잘 예측했다고 해보자. 그러면 loss가 쌓이지 않을 것이다.(대입해봐라.), # 1과 가깝게 예측될 수록 loss가 덜 쌓일 것이다.
yi가 1인 경우, ^yi가 0에 가깝게 예측됐다면 cost가 생길 것이다.
즉 정답과 가깝게 예측했다면 loss가 덜 쌓이는 구조이다. 이 함수는 자주 쓰니까 꼭 외위놓자.

cf) Loss function을 다 더해서 평균낸게 cost function(J(w))
'학부 수업 > 데이터마이닝' 카테고리의 다른 글
| 6. Random Forest (3) | 2024.05.20 |
|---|---|
| 5. Decision Tree (4) | 2024.05.20 |
| 3. K-Nearest Neighbors (KNN) (1) | 2024.05.20 |
| 2. Supervised Learning(지도 학습) (0) | 2024.05.20 |
| 1. Introduction 데이터 마이닝이란? (3) | 2024.05.20 |