7. Support Vector Machine with hard-margin

7주차. Support Vector Machine

 

서울시립대학교 인공지능학과 노영민 교수님의 데이터 마이닝 강의를 정리함을 미리 알립니다.

• Support Vector Machine(,SVM)이란..

SVM은 고차원 데이터셋을 이진 분류에 강력한 일반화 성능을 보임이 입증된 모델로,  훈련 과정에서 이차계획법(quadratic programming problem)을 해결하는 형태로 학습이 진행된다.

 

SVM은 목적 함수 목적함수(, Decision function )의 일반화 성능을 최대로 하도록 훈련하며, 통계적 학습 이론에 기초를 둔다.

 

이렇게 말하면.. 선형 계획법, 이차 계획법에 대한 선행 지식이 없을 때 사실 이해하기 어렵다....

우선 우리가 뭘 하려는지를 알고, 관련 개념들을 알아가며 SVM에 대해 이해해보자.

 

우리는 고차원 데이터셋에서 '이진 분류'를 하고 싶다..! 다음과 같이 3차원 공간에 훈련 데이터가 있다고 하자.

파란 공이 class1, 빨간 공이 class2라고 하자.

우리는 두 class를 분류하고 싶다. 이를 위해 decision boundary를 세워야한다.

고차원에서는 이 경계가 초평면 (,hyperplane)  $ W^T + b = 0 $으로 표현될 것이다.

벡터 $ W $는 당연히 이 초평면의 법선 벡터(normal\ vector)이다.

우린 이제  클래스를 구분하는 초평면들 중 어떤 것이 가장 좋은 초평면인지 알아야한다.

클래스를 구분하는 여러 초평면들이 그려졌다고 가정하고, 그 옆면에서 이를 바라봐보겠다.

실선이 hyperplane을 옆에서 바라본 모습이다.

어느 한 class에 너무 가깝지 않고, 각 클래스를 균등하게 잘 나눠야 새로운 데이터에 대한 일반화 성능이 높을 것이다.

왜 일반화 성능이 높을 지는 직관적으로 생각할 수 있다. 균등하게 나누지 못한 1번 초평면이 선택된다고 하면 class 1과 가깝고, class 2와 멀지만 class 2로 분류되는 경우가 생길 것이다.. # 균등하게 나누는 초평면이 좋은 초평면..

4개의 초평면 중 3번 초평면이 가장 좋은 초평면이다.

즉, 우리는 두 범주를 여유있게 나누는 초평면(Optimal-Plane)을 선택해야한다. 이를 Margin를 최대화한다 라고 표현한다.

# SVM의 목표는 훈련 데이터에 대해 margin을 최소화 (= 일반화 에러를 최소화 = 좋은 예측 성능) 이다.

좀 다르긴 하지만 여유를 margin이라고 생각하면 쉽다... 

 

각 클래스를 균등하게 나누기 위해 우리가 최대화할 Margin이 무엇인지 정확하게 알고 넘어가자.

 

 

• Margin? (Geometric 관점)

Margin이란 hyperplane $W^TX + b = 0$에서 $ |W^TX + b| = 1 $ 까지 떨어진 법선 방향의 거리를 의미한다. 

이 margin을 최적화하기 위해 수식을 만들기 위한 margin을 정의할 것이다.

이를 이해하기 위해 두 평면 plus - plane, minus - plane을 두고 평행한 세 평면을 기하적으로 확인해보자.

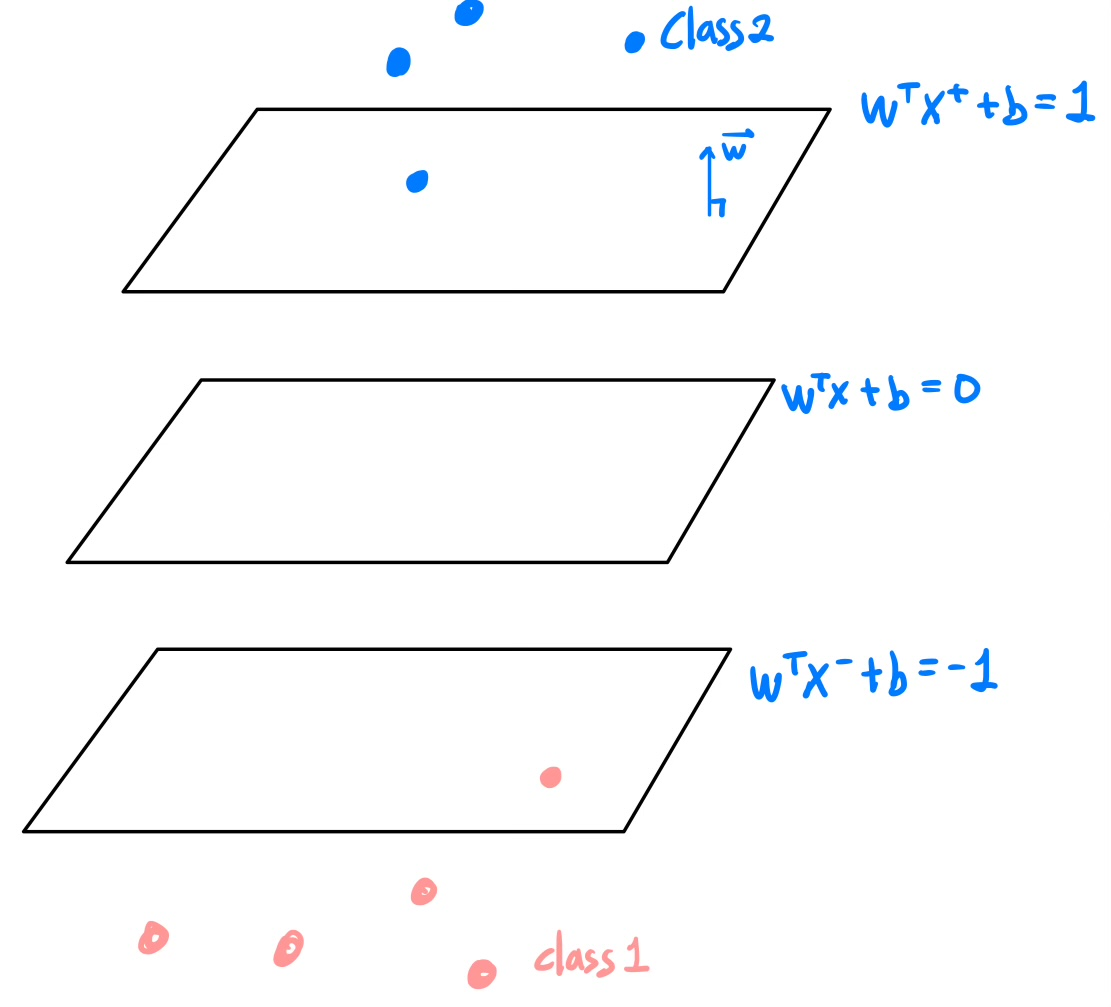
Plus - plane : $ W^TX^+ + b = 1 $

Minus - plane : $ W^TX^- + b = -1 $

 

세 평면은 평행하므로 벡터의 시점이 어디든지  $ X^+ = X^- + λW $ 임을 알 수 있다.

이를 통해 다음 과정으로 Margin을 정의한다.

margin을 수식화.

$ X^+ = X^- + λW $ 를 plus-plane에 대입하여 λ에 대한 정보를 우선 얻었다. 이후 margin의 정의 $W^TX + b = 0$에서 $ |W^TX + b| = 1 $ 까지 떨어진 법선 방향의 거리를 $||X^+ - X^-||/ 2$ 로 표현하여 margin을 표현했다.

 

즉 Margin을 수식으로 표현하면 다음과 같다.

$$ Margin = 1 / ||W||_2 $$

 

 

• Maximize Margin

우리는 이러한 Margin을 최대로 하면서, 동시에 훈련 데이터에 있는 모든 class를 구분해야 한다(이진 분류).

이를 위한 최적화 식을 만들 것이다.

1) 목적함수를 계산이 편하도록, 역수를 취해 Minimize로 바꿔준다. 1 / ||W||_2 는 양수이기에, 뒤집고, 제곱하고, 상수배를 해도 괜찮다. (Max -> Min 문제로 변경됨). 또한 L2-norm은 제곱근 때문에 계산이 어려우므로 제곱을 한다

2) binary variavle $y_i$ 를 도입한다.

최종 최적화 식은 다음과 같다. 

이게 바로 이차 계획법이다. 이를 해결하는 형태로 학습을 진행한다. 

이러한 이차 계획법은 Optimal solution이 존재한다.

# 해당 최적화식은 훈련 데이터가 Linearly separable한 경우만 해가 존재한다(hard-margin). 즉 한 초평면으로 모든 class를 구분할 수 있을 때를 말한다. Linearly separable하지 않은 경우(soft-margin) 는 다음 강의에서 공부할 예정이다.

 

이러한 이차 계획법을 해결하는 형태로 훈련을 진행하면 이진 분류와 함께 margin을 최대로 하는 과정에서 다음과 같은 결과가 나온다.

38선 사이에 같은 길이의 여백(margin)이 있다고 생각하면 쉽다..

두 클래스를 구분하고 margin을 최대로 하기 위해 필연적으로 plus-plane과 minus-plane 위 데이터가 존재할 것이다. 이 벡터들이 바로 Support vector이다.

참고) plus-plane과 minus-plane에 데이터가 존재하지 않다면, 데이터를 만날 때 까지 margin을 늘릴 수 있으므로 margin이 최대가 아닌 것이다. 그렇기에 margin을 최대로 하면 plus-plane과 minus-plane 위 데이터가 존재하는 것이다.

 

 

• Lagrange Dual formulation

우리는 위 최적화식을 풀기 위해 Lagrangian multiplier를 이용하여 Lagrangrian primal 문제로 변환한다. 

이렇게 구해진 LP가 Convex, continuous이기에 임계점에서 최대. 최소를 갖는 점을 이용하여 Lagrange Dual formulation를 만든다.

Lagrange Dual formulation 알파에 대한 식으로 표현됐다. 알파는 데이터 갯수 만큼 존재한다.

풀이는 아래 첨부한다. (엄밀하지 않으므로 시험용..으로 외워두자.)

 

구한 (w, b, α)가 Lagrange Dual formulation의 최적해가 되기 위해 다음과 같은 조건을 만족해야 한다. #KKT conditions

수학적으로 증명된 것이니 시험을 위해 외우면 된다..

우선 임계점이 보장되어야 한다(Stationarity). dual를 만들기 전을 primal이라고 하는데, 이 때의 제약식을 만족해야한다(primal feasibility), 또한 dual 문제의 제약식을 만족해야 하며(dual feasibility), 마지막으로 Complementary slackness를 만족해야 한다.

2번, 3번 조건..은 primal과 dual에서 온다.

# Complementary slackness 제약식을 통해 support vector를 알 수 있다.

lp를 만들기 위해 도입한 알파값을 통해 support vector를 구분할 수 있다.

support vector가 아니면 알파 값은 0이 되므로, 서포트 벡터일 때만 값을 가진다. 즉 서포트 벡터만 이용하여 구하고싶은 초평면을 구한다.

훈련 데이터를 통해 Margin을 최대로하며 모든 훈련데이터를 완벽하게 분류하는 W*과 b*를 구하였고, 이를 통해 새로운 데이터에 대한 예측을 시도할 수 있다.

sign 함수는 $ W*^TX_{new} + b* >= 0$ 이면 +1( ,class 2 )를,  sign 함수는 $ W*^TX_{new} + b* < 0$ 이면 -1( ,class 1 )를 함수값으로 가질 것이다.

 

Margin을 다음과 같이 한 번 더 계산할 수 있다.

margin의 제곱이 모든 알파 합의 역수가 된다.