8. Support Vector Machine with Kernel Trick

8주차(2). Support Vector Machine with Kernel Trick

 

서울시립대학교 인공지능학과 노영민 교수님의 데이터 마이닝 강의를 정리함을 미리 알립니다.

 

Linearly Non-separable Problem에서 어느정도의 훈련 데이터 에러를 허용하여 Decision boundary인 초평면을 결정할 수 있었다(SVM with soft margin). 아래 예시처럼 train error가 너무 높을 수도 있다.

주황색 선이 soft margin SVM을 이용해 만들어낸 초평면, 노란색이 error라고 보면 된다.

이 때 모델을 복잡하게 해서 = Parameter 갯수를 늘려서 Nonlinear Decision boundary를 만들면 되긴 한다...

하지만.. 우리는 Linear Decision boundary를 사용하면서 해당 문제를 해결할 수는 없을까?? 이렇게 해결하기 위해 사용하는 mapping function과 Kernel에 대해 알아볼 것이다.

 

 

• mapping function

mapping function은 저차원의 input vector를 고차원 공간의 벡터로 변경하는 함수이다.

맵핑 함수 적용 예시 1 (변경된 차원 6차원에 대해.. 4차원 이상은 그리지 못하므로 축은 2개만 그렸다..)

 이 맵핑 함수를 사용하여 기존의 데이터를 고차원에 적절하게 배치하면, 선형 경계로 나눌 수 있을 것이다.

맵핑 함수 적용 예시 2

2차원에서 선형 결정 경계를 갖지 못하던 데이터가 적당한 맵핑 함수를 이용하여 3차원으로 재배치하니까 선형 경계(초평면)로 구분할 수 있게 되었다. 이게 바로 맵핑 함수의 역할이다. 이렇게 옮겨진 새로운 차원을 Kernel Space라고 한다.

맵핑 함수 적용 예시 3 Kernel space에서 관측치의 분류가 더 쉬울 수 있다.

 

 

 

 

• Kernel Mapping # Kernel Trick

고차원 Kernel space는 관측치 분류가 더 쉬울 수 있고, Kernel space를 효율적으로 계산할 수 있는 방법(Kernel Trick)이 존재하기 때문에 우리는 SVM을 기존의 공간이 아닌, Kernel space에서 학습할 것이다. ***

 

방법의 soft margin SVM과 같다. 하지만 기존 데이터 & x_i &를 맵핑 함수에 대입하여 사용하는 것이 다르다.

LP

기존의 soft margin SVM에서 x만 맵핑하면 된다.

맵핑 함수는 위 적용 예시처럼 매우 매우 복잡하다. 이를 그대로 계산하기 힘드니 우리는 Kernel 함수를 사용한 Kernel Trick를 도입한다. Kernel function이란 맵핑하기 전의 데이터의 함수로, 맵핑해서 내적한 결과가 된다. 이러한 과정이 Kernel Trick이다.

커널 함수란 맵핑된 데이터의 내적을 기존의 데이터를 활용해 쉽게 계산하는 함수라고 생각하면 됨.

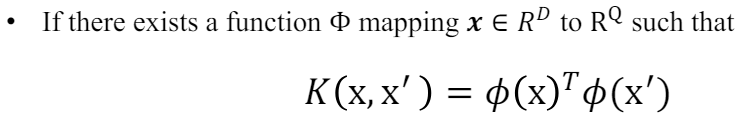
이를 라그랑즈 듀얼에 도입하여 문제를 해결할 것이다.

 

Kernel Trick을 통한 학습 과정..

Kernel Trick의 예시

 

이러한 커널 함수는 여러 종류가 존재한다. 아래 3가지는 꼭 암기하자.

이러한 커널 함수를 사용하면 맵핑된 데이터의 내적을 쉽게 계산할 수 있다.

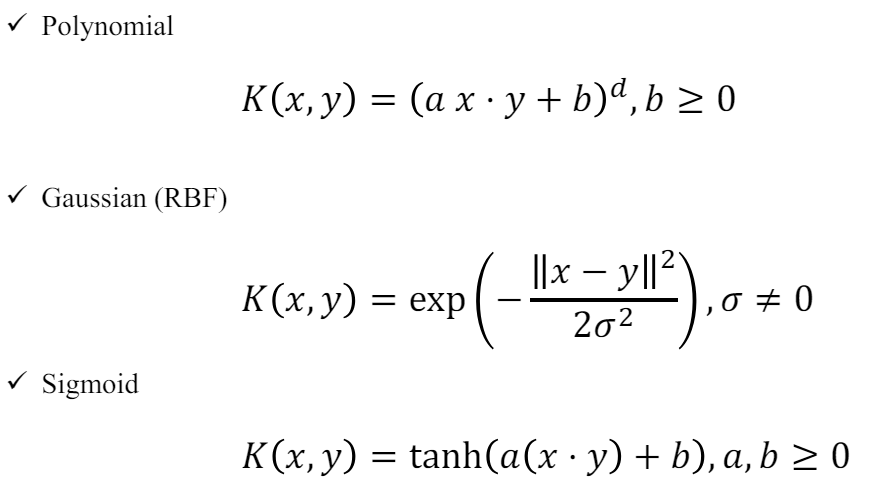
특히 RBF는 Taylor 전개를 통해 이론적으로 무한 차원으로 보냄을 보일 수 있다.

참고..

위에서 Kernel Trick를을 사용하여 복잡한 내적 계산을 하지 않고 SVM을 고차원(Kernel Space)에서 훈련시킬 수 있었다.

이제는 학습된 모델로 예측을 하는 과정을 알아볼 것이다.

 

 

• Prediction of SVM with Kernel Trick

우리는 결정 경계을 위와 같은 방법으로 결정했었다.( S.V에 관련된 평균..) 하지만 맵핑된 경우에 이런 방법을 그대로 사용하면 복잡한 내적 계산이 생긴다... 우리는 Kernel Trick을 사용해야한다.