서울시립대학교 인공지능학과 김정연 교수님의 확률 및 랜덤 프로세스 강의를 정리함을 미리 알립니다.
Ch2. 확률론의 기본
<Outlines>
1. 확률 실험
2. 확률
3. 경우의수
4. 확률의 공리
5. 조건부 확률
6. 사건의 독립
7. 유사 난수 발생기
1. 확률 실험
확률 실험은 실험이 다음과 같은 조건에서 반복될 때, 그 결과가 예측할 수 없는 방식으로 변하는 실험이다. 확률 실험은 실험 절차와 하나 이상의 측정이나 관찰들에 대해 자세히 기술되어야 한다.
- 실험(Experiment): 어떤 현상의 관찰 결과를 얻기 위한 과정

확률 실험은 일관되게 같은 결과를 내지 않기에, 가능한 결과들의 집합을 결정해야 한다.
모든 관찰 가능한 결과의 집합을 표본 공간(sample space)라고 한다. 이러한 표본 공간을 셀 수 있으면 이산 표본 공간, 셀 수 없으면 연속 표본 공간이라고 한다.
- 표본 공간(sample space): 관찰 가능한 모든 결과의 집합
-> 이산 표본 공간(discrete sample space): 셀 수 있는 표본 공간
연속 표본 공간(continuous sample space): 셀 수 없는 표본 공간
- 사건: 표본 공간의 부분 집합.
모든 결과를 포함하고 있어 항상 발생하는 확실한 사건과, 결과를 전혀 포함하고 있어 결코 발생하지 않는 불가능한 사건 또는 공사건으로 나뉜다. (걍 그렇군.. 하고 넘어가면 됨.)

그냥 용어 설명하는 단원이라 걍 그렇군 하고 넘어가면 된다.
표본 공간이 관찰 가능한 모든 결과의 집합임을 기억하자.
2. 확률
cf) 집합 이론의 복습 - 그냥 헷갈릴만 한거만 보고 넘어가자.
1) 분배 법칙과 결합 법칙을 구분하라.

당연한 것 같지만.. 분배 법칙 좌변에 결합 법칙 쓰는 바보 같은 짓 할 수 있다. 조심하자. 기호가 같을 때 결합 법칙을 사용할 수 있다.
2) 교집합 서로소 (배반, disjoint)
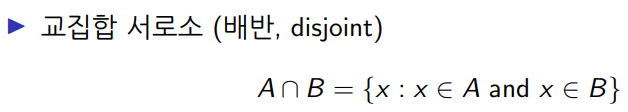
너무 쉬운 개념이지만.. 뒤에 계속 '배반'에 관련된 내용이 나올거니까 음 이런거였지 보고 넘어가자.
- 등확률모형(equal probability model, uniform proabability model)
임의의 사건 A에 대한 확률이 다음과 같이 주어지는 경우이다.

그니까 원소 갯수 하나 당 확률이 같은거지..
ex) 주사위 눈금이 짝수가 나올 확률.. A = {2, 4, 6}, S = {1, 2, 3, 4, 5, 6} P(A) = |A| / |S| = 3/ 6
- 근원 사건(elementary event): 표본공간 S의 각 원소 s ∈ S로 이루어진 사건 {s}.
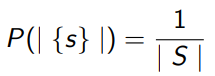
그니까 표본 공간의 원소 하나 뽑는 확률이 1/ |S|인 것.. ex) 주사위 눈금 1 뽑기, 주사위 눈금 2 뽑기... 이런게 근원 사건인거다.
그렇군! 계속 용어 정리만 하고 있다.
3. 경우의 수
곱의 법칙, 순열, 조합을 통해 경우의 수를 계산한다. (고등학교 수학이니 개념 설명은 생략한다.)
혹시 모르니까 **공식**만 외워놓고 있자..
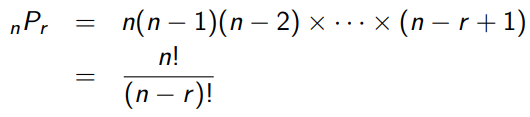
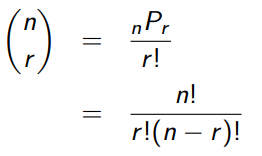
cf) 사실 조합은 쓰레기 기호이다. 저거 왜 쓰는지 모르겠다. 순열로 뽑고, 순서를 부여해주면(x r!) 끝이다.
이와 마찬가지로, 순열은 조합에서 순서를 배제(%r!)한거다.
<Example>

ex1_sol) 너무 간단하지.. 5C2 = 5*4 / 2*1 = 10.
*ex2_sol) 한 묶음 50에서 10개를 뽑는데, 정상품 40개에서 7개 그리고 불량품 10개에서 3개를 뽑는 조건부 확률로 보면 좋다. (잘 모르겠으면 걍 유형을 외워라).P = (특정 경우의 수/ 10개를 뽑는 전체 경우의 수)
= 10C3 * 40C7 / 50C10
- 이항정리
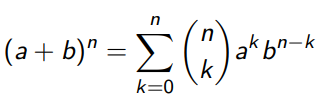
만약 a = b = 1인경우, 1의 지수승은 모두 1이므로 다음이 성립한다.
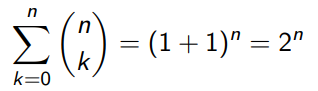
- 다항정리

걍.. 너무 고민할 것 없이 이항 정리만 챙겨가자.
# 이항 정리의 **증명**
이는 조합을 통해 증명할 수 있다. (엄밀한 증명은 아니다. (a+b)^3에서 이항정리 공식과 같음을 보이겠다.)

사실 엄밀한 증명은 아니니까... 걍 이렇게 증명하면 되는구나 넘어가라. 수업 때 증명해주셔서 혹시 몰라서 넣어놨다.
4. 확률의 공리

그냥 읽어보면 당연할 것이다. 음 당연하군! 읽으면서 하고 넘어가자.

# 확률의 성질

# 확률의 성질 증명 **
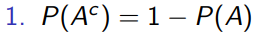

A와 A의 여집합의 교집합은 당연히 공집합이다.
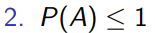
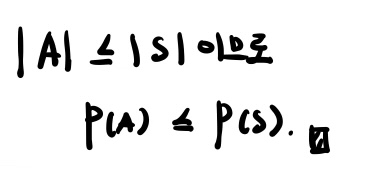
3번은 자명하다.


5번은 벤다이어그램으로 간단하게 증명할 수 있다.
6번은 자주 사용하지 않으므로 생략한다.
7번 또한 벤다이어그램으로 간단하게 증명할 수 있다.
<Example>

그냥 풀면 된다.. 여기서 봐야할 것은 3개의 합집합을 구하는 공식이다.
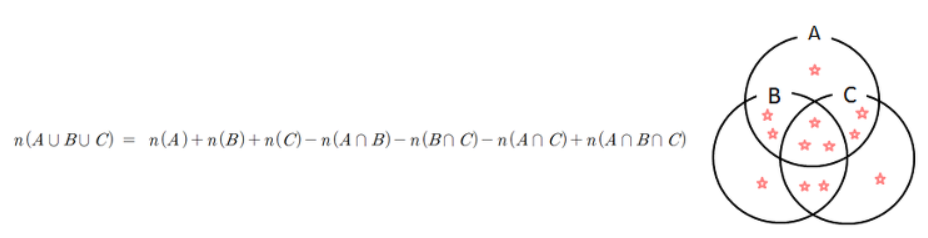
위는 A, B, C의 합집합 원소를 세는 방법이다. 확률도 이와 같이 중복된 교집합에 대해 보정이 필요하다.
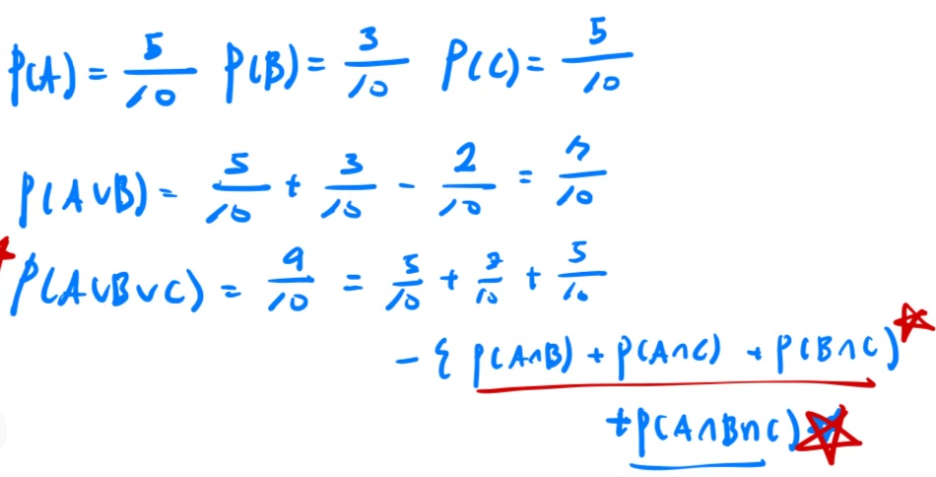
5. 조건부 확률 ****** 매우 매우 중요... 베이즈 정리 등.. 이쪽 파트 문제를 많이 풀어봐야한다.

- 조건부 확률의 성질(1)*** # 교집합을 조건부 확률로 표현할 수 있다. # 어떤 조건부인지는 니가 선택하라.

조건부 확률의 성질1... 교집합 = 니맘대로 조건부 확률
이 성질을 통해 교집합을 구하기 어려울 때, 조건부 확률을 통해 교집합 확률을 구한다.
# 교집합 확률 구하기 어렵다? -> 조건부 확률 성질1을 떠올리자.
****<Example>****
-> 성질(1) 이용 유형 Tree Diagram ***작년 기출.. 암기 유형...****
바로 교집합의 확률을 구하기 어렵다. 이 때 Tree Diagram을 그려 조건부 확률을 표현하고, 이를 통해 우회적으로 교집합의 확률을 구한다.

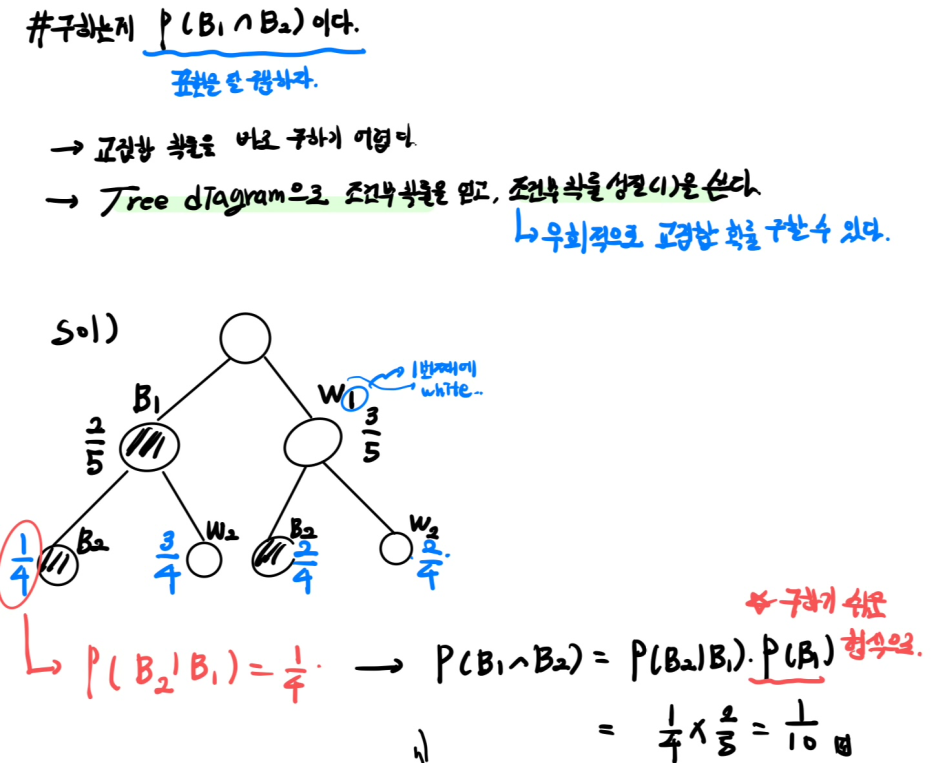

교집합을 바로 구하기 어려우므로, 조건부 확률의 성질(1)과 Tree diagram으로 해결한다.
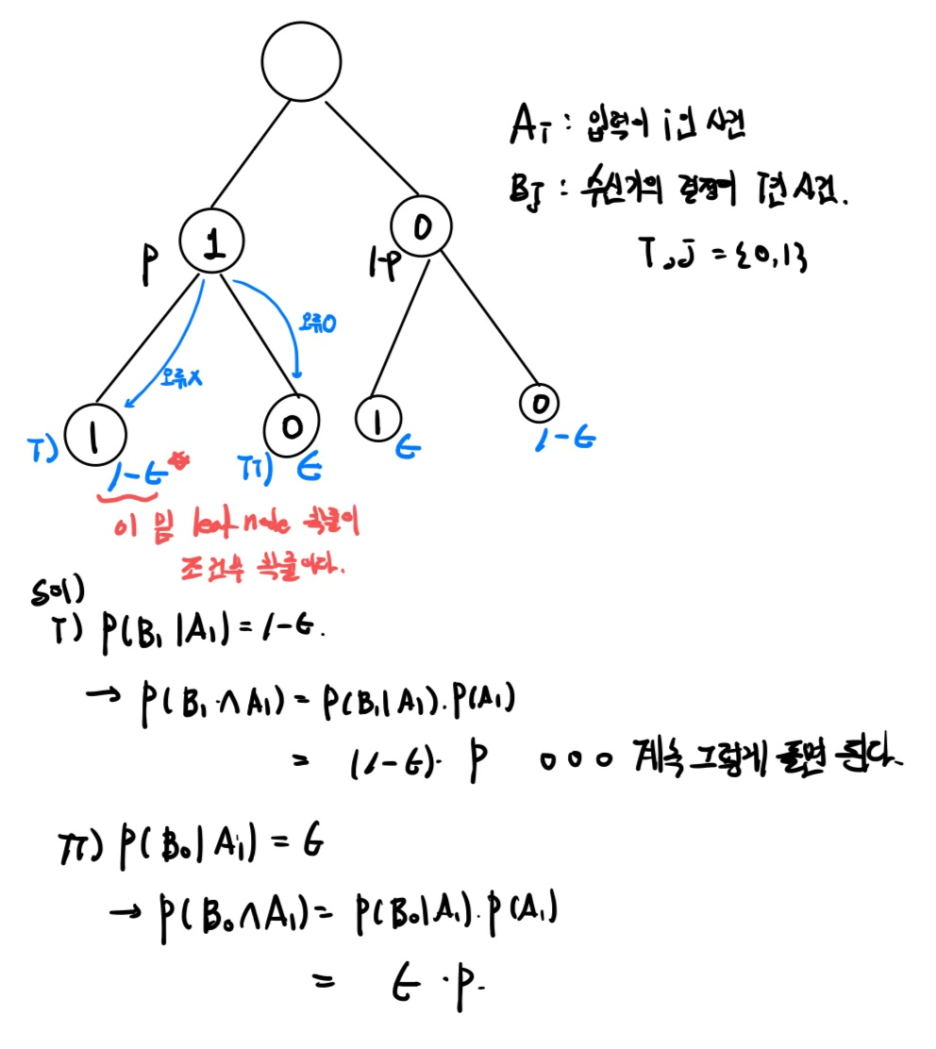
*Tree의 leaf node는(맨 끝) 조건부 확률임을 기억하라.
- 조건부 확률의 성질(2) # 배반일 때 # 그냥 차분하게 전개하면 된다.

A1과 A2가 배반사건일 때 성질(2)가 만족됨을 조심하라.
그냥 A1과 A2가 배반사건이라 교집합이 없다. 그래서 조건부 확률의 합집합에서도 더하기로 표현이 가능하다..
cf) 이는 벤다이어그램으로 증명하면 간단하다.
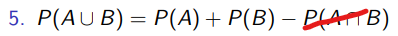
이거의 조건부 확률 버전이라고 생각하면 쉽다.
음 그렇군!
- 표본 공간의 분할
이제 가장 중요한 공식을 배울 것이다. 이를 위해 표본 공간의 분할에 대해 알아보자. 이는 간단하다 말 그대로 표본 공간을 분할한다. 이 때 중복이 없도록 배반 사건으로 표본을 분할하는 것이다.
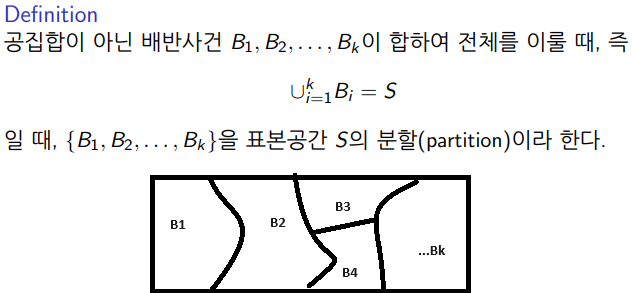
꼭 배반 사건으로 분배 해야한다. 모든 땅에 대해 땅따먹기를 한다고 생각해라!!
- *******전확률 공식******** # 교집합 전체 합을 조건부 확률로 바꾸는 느낌 # 배반일 때 쓰는거다!!
표본 공간이 배분되었을 때(= 조건이 상호 배반일 때) 임의의 사건 A에 대하여, 다음이 만족한다.

이는 그림으로 더 쉽게 이해할 수 있다. 표본 공간 S를 배반사건 B1, B2 ,B3 ,B4로 분할(partition)했다고 하자.

사진 설명을 입력하세요.
우린 여기서 P(A)가 알고싶다.
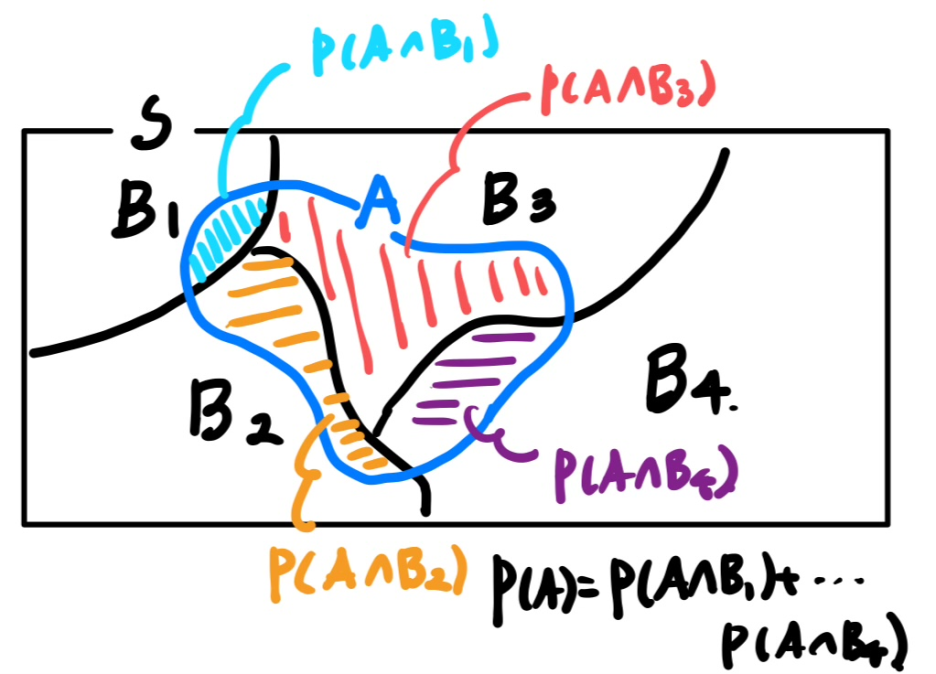
P(A) = P(A∩B1) + P(A∩B2) + P(A∩B3) + P(A∩B4)라고 볼 수있다. 사건 A의 확률 알고 싶어 모든 교집합을 구하고 싶은데 바로 구하기 어려워 조건부 확률을 사용하는게 바로 전확률 공식이다. 단독 사건 확률을 배반 사건의 조건부 확률 합 로 구할 수 있다.
조건부 확률 성질(1)에서 교집합 확률을 구하기 어려워, 조건부 확률을 사용했다. 이를 기억하라.
B가 배반사건일 때 사용하는 공식이다. 이를 꼭 까먹지 마라. 배반이 아니면 중복된 경우가 발생된다.
# 전확률 공식의 증명 ***

단독 사건의 확률을 배반 사건의 조건부 확률 합으로 표현했다.
<Example> **

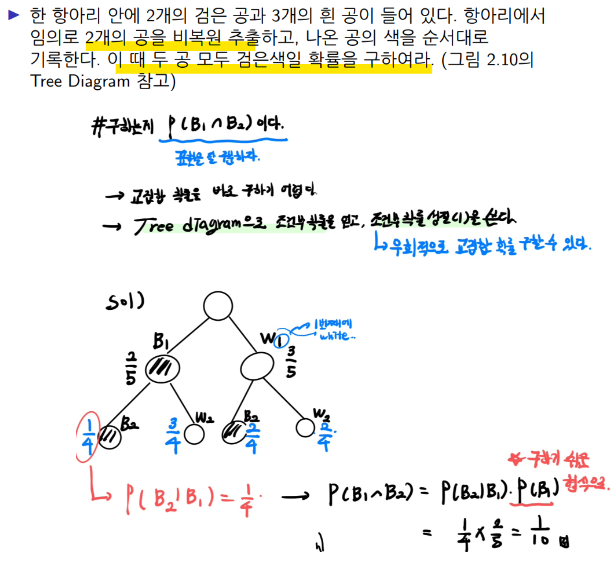
위에서 풀었던 예제 2.25
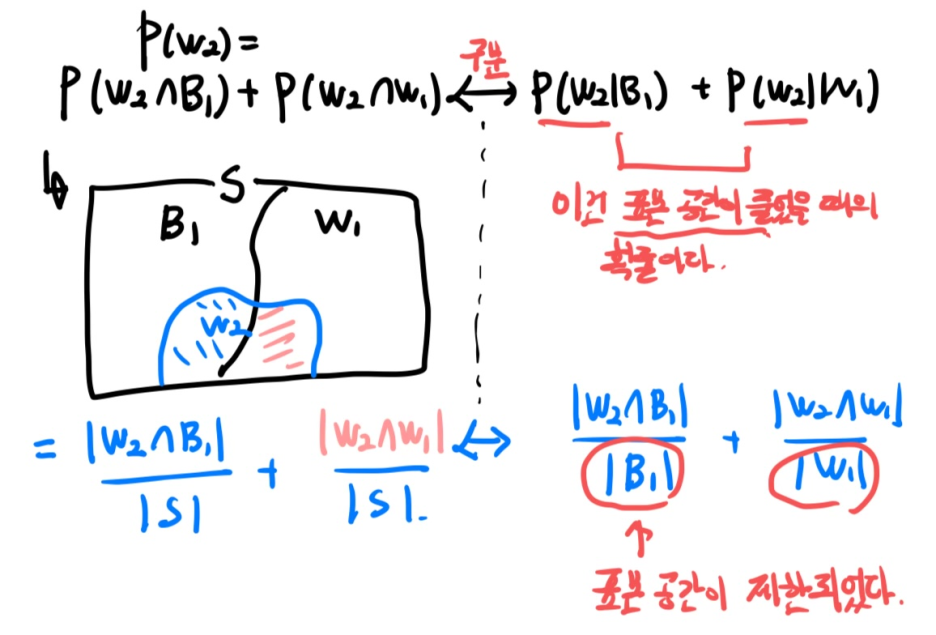
우리가 구하고 싶은 건 P(W2)이다.
P(W2) = P(W2∩B1) + P(W2∩W1)로 볼 수 있다. B1 과 W1는 전체 표본 공간을 분할하는 배반사건이다. (생각을 해봐라 당연하다.) 이는 전확률 공식으로 인해 P(W2|B1)P(B1) + P(W2|W1)P(W1)으로 구할 수 있다.
cf) 시험 대비
단독 사건의 확률을 조건부 확률의 합으로 구하는 유형이라고 생각해라. Tree diagram 문제가 나오면 윗 예제에 더 이어서 이걸 물어볼 것이다.
Tree diagram에서 맨 끝 노드는 조건부 확률이었다. 이를 통해 교집합을 구하는 유형이 있었다. (방금 풀었잖아 조건부확률 성질(1)에서) 이걸 모든 배반 사건에 대해 다 더해 단독 확률을 구하는 것이다.
cf) 헷갈리는 내용!! # 교집합과 조건부 확률의 차이.
아니 첫 번째 공 검은색이고 두 번째 공 흰색인 거랑 P(W2∩B1) <-> 첫번째 공 검은색일 때, 두번 째 공 흰색인거랑P(W2|B1) 차이가 뭐냐?? 그냥 말만 다르고 같은 의미 아니냐? 생각할 수 있다. 이 차이는 표본 공간을 잘 보면 된다. 확률이 계산되는 표본 공간이 달라진다. (조건부 확률은 표본 공간이 작아진다.)
- 베이즈 법칙 # 조건부 확률의 조건 순서를 뒤바꾼다. # 분모에는 전확률 공식이 들어간다.
이걸 언제 쓰느냐를 아는 것이 가장 중요하다. 만약 우리가 조건부 확률 P(A|B)가 알려져있거나 쉽게 알 수 있다고 하자. 이 때 우리는 B가 아닌 A가 전제인 P(B|A)를 알고 싶다 할 때, 베이즈 법칙을 사용할 수 있다. 즉 베이즈 법칙을 통해 조건부 확률의 전제를 바꿀 수 있는 것이다.

베이즈 정리 또한 전확률 공식이 들어가므로 B가 배반사건이어야 사용할 수 있다. cf) 조건부 확률 성질(2)부터 지금까지 계속 배반 사건의 개념이 들어갔다. 잘 확인하자.
<Example>***


우리는 P(B|A)는 끝 노드를 활용해 쉽게 구할 수 있지만, P(A|B)는 쉽게 구할 수 없다. 이럴 때 바로 베이즈 정리를 사용하는 것이다.
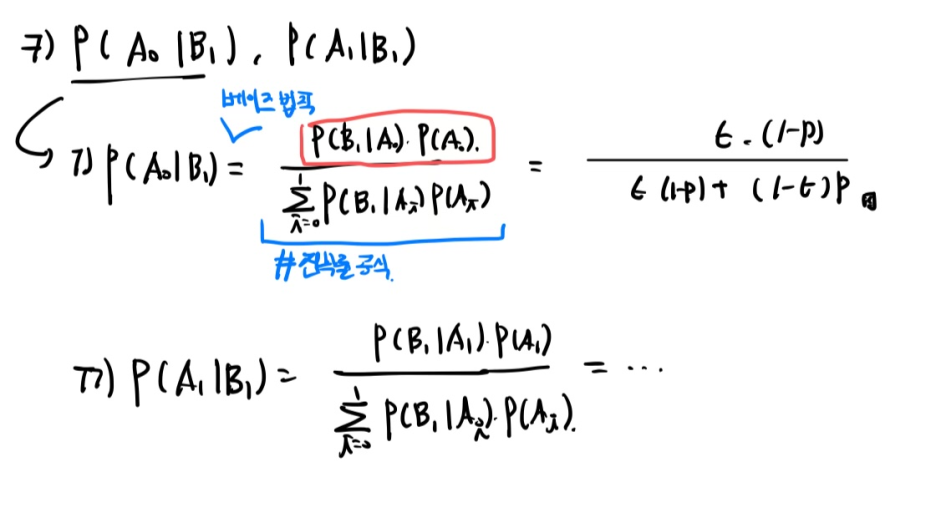
A는 당연히 배반사건이다. 여러 번 풀어보자.
6. 사건의 독립
- 독립의 정의
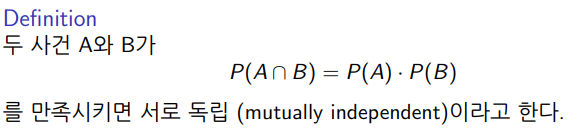
독립의 정의.
독립의 정의는 매우 쉽다. 두 사건이 독립적으로 일어나 서로 영향을 주지 않는거다. 두 사건이 독립인 걸 보이는건 두 교집합의 확률이 각 확률의 곱과 같음을 보이면 된다. # P(A∩B) = P(A)P(B)
<Example>

sol) 사건 A, B가 독립임을 보이기 위해 P(A∩B) = P(A)P(B)임을 보이면 끝이다.

A와 B는 독립이다. ( 1/2 * 1/2 = 1/4 ) 하지만, A, C는 독립이 아니다.

각 원소를 뽑는 확률이 같다고 생각한다. (등확률 모형) 그렇기에 확률을 해당 면적 / 전체 면적으로 볼 수 있다.
위 예제는 사건이 2개다. 사건이 3개 이상이 될 때도 똑같이 적용하면 된다. 다음과 같이 일반화 할 수 있다.

독립 정의의 일반화. 사건이 몇 개든 그냥 교집합과 곱 확률이 같으면 독립이다.
- 독립의 성질 ****시험 대비***

1번 성질 증명을 잘 외워놓자. 드모르간 공식과 곱셈법칙을 통해 증명한다. (약식 증명 사건이 2개일 때만..)

약식 증명이다. 시험에 나올 수 있으니 잘 해놓자. 중간에 곱셈 법칙이 들어가는게 포인트다.
<Example>


각 고장은 독립적으로 일어났다. 즉 각 시행의 결과가 다른 시행의 결과에 영향을 주지 않는다.
- 곱 실험

걍 읽어보기
- 독립 시행

걍 읽어보기. 당연하다.
7. 유사 난수 발생기 (week4 다시 나올 것이다)
'학부 수업 > 확률 및 랜덤 프로세스' 카테고리의 다른 글
| ch5. Pair Of RVs(2) - 이변량 정규분포 (0) | 2024.05.13 |
|---|---|
| ch5. Pair Of RVs (0) | 2024.05.09 |
| ch4-2. simulate RV (0) | 2024.05.09 |
| ch4. Continuous (2) | 2024.05.09 |
| Ch3. Discrete (1) | 2024.05.09 |