서울시립대학교 인공지능학과 김정연 교수님의 확률 및 랜덤 프로세스 강의를 정리함을 미리 알립니다.
Chapter 04-2. 확률변수의 생성
<Outlines>
1. 몬테칼로 방법
2. 유사난수 발생기-선형합동수열
3. 역변환법, 합과 혼합 변환법
5. 채택-기각법
1. 몬테칼로 방법(Monte Carlo method)
만약 PDF fx로 부터 랜덤 표본을 생성하는 것이 가능할 때, 생선된 표본을 바탕으로 추론하는 방버.
# 표본 뽑아서 모집단 정보 알고싶다.

PDF로 부터 랜덤 표본을 뽑는다. 이에 대한 실험적 분포(empirical distribution)은 m이 커짐에 따라 fx로 수렴함.
음 뭔가 와닫지는 않는다.. 그니까 표본 데이터를 통해 모집단의 정보를 알고 싶다는거다..

걍 음 그렇군..
이제 샘플을 생성하는 법을 배울 것이다...
2. 유사난수 발생기-선형합동수열

음 다음 항에 전 항 선형변환의 m으로 나머진 나머지를.. 이렇게 하면 난수가 유사 난수가 나온다.
# 알고리즘

나누는 m값이 주기와 나타내는 수를 정한다. 위 예제에서 m = 100이었으므로 초기값 0부터 99(m-1)가 주기 100을 따라 나타난다.
3. 역변환법
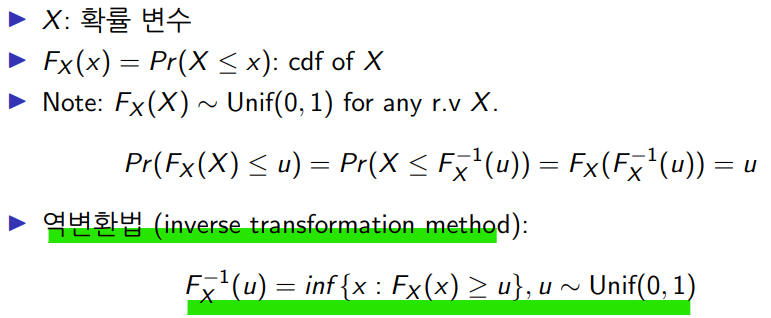
Q. 역 변환법이 정의를 기술하라.
# cf) CDF의 역함수의 정의를 생각하라.

비슷한데, 대입값 모양만 좀 다르다..
정형화된 분포에서 난수를 발생했다. 이정도 알고 걍 코드나 외우자.. 이에 대한 의미는 기말고사 범위에서 다룰 것이다. (이걸 어디다가 써먹는지..)
4. 채택-기각법 ***증명***
fx 즉 pdf를 알지만 E(X), Var(X)를 구하기엔 식이 너무 복잡하고, 샘플링 또한 어려울 때, 샘플링할 수 있는 다른 pdf gx를 통해 fx의 표본을 채택한다. 이걸 채택- 기각법이라고 한다.
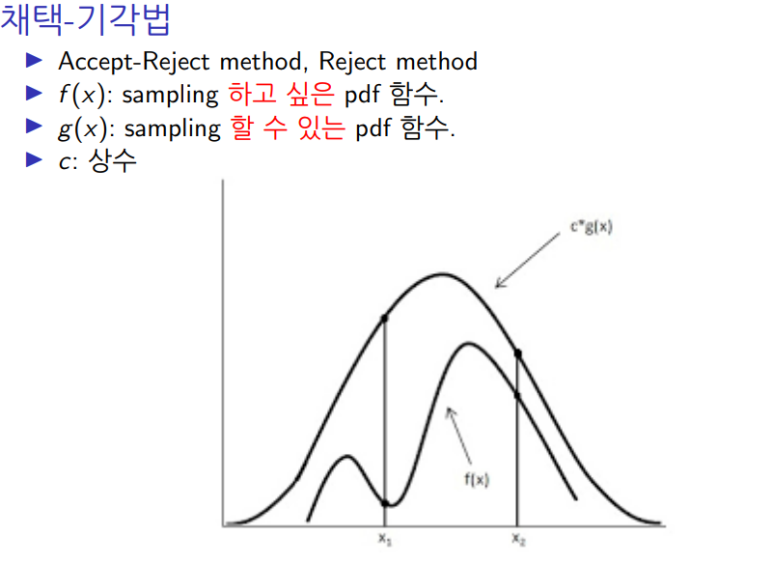
의미를 잘 알아두자.
- 채택 기각법 알고리즘 **암기** (중간고사 기출)
1) pdf gx로 부터 표본 xi 생성
2) unif(0, 1)로 부터 표본 u 생성
3) 만약 u <= f(xi)/cg(xi)라면 xi를 fx의 표본으로 채택/ u> f(xi)/cg(xi) 이면 기각.
채택 기각법 증명

# 알고리즘

'학부 수업 > 확률 및 랜덤 프로세스' 카테고리의 다른 글
| ch5. Pair Of RVs(2) - 이변량 정규분포 (0) | 2024.05.13 |
|---|---|
| ch5. Pair Of RVs (0) | 2024.05.09 |
| ch4. Continuous (2) | 2024.05.09 |
| Ch3. Discrete (1) | 2024.05.09 |
| ch2. Probability (2) | 2024.05.09 |