서울시립대학교 인공지능학과 김정연 교수님의 확률 및 랜덤 프로세스 강의를 정리함을 미리 알립니다.
Chapter 06. 벡터 확률 변수
<Outlines>
1. Random vector
2. 확률변수들의 함수
3. 기대값
4. 적률생성함수
1. Random vector
- Random vector
n개의 확률 변수를 다루기 위해 우리는 Random vector(확률 벡터)를 사용한다.
사건을 맵핑하는 함수라고 설명한 Random Variable(확률 변수)가 열 벡터로 존재하는 것이다.

Random Vector 안에는 확률 변수들이 존재하므로, cdf, pdf는 결합 cdf, pdf이다.
- Random Vector(확률 벡터)의 결합 PDF, CDF


걍 그렇군..
이산형의 경우 PDF의 함수 값이 확률이다. 그렇기에 이를 누적해서 더해주면 CDF가 된다.
연속형의 경우 PDF의 함수 값은 확률의 값이 아니다. 하지만 이를 적분해서 CDF를 구하면 된다.
- Random Vector(확률 벡터)의 주변부 PDF (Marginal PDF)

확률 변수가 2개일 때랑 같다. 확률 벡터 성분 중 알고 싶은 확률 변수만을 제외하고, 전구간 연산을 하면 된다.
- Random Vector(확률 벡터)의 조건부 확률 밀도 함수 (조건부 PDF) ****
확률 변수가 2개일 때의 조건부 확률 밀도 함수는 다음과 같이 구했다.

그냥 간단하게 분자에는 결합 pdf가, 분모에는 조건부에서 사용되는 확률변수 pdf를 넣어주면 된다.

확률 벡터에서도 분자에는 결합 pdf를, 분모에는 조건부에 사용되는 확률변수들의 결합 pdf를 넣어주면 된다.

예시를 통해 알아보자...
** <Example 6.7> **

우리가 구해야하는건 i) 확률 벡터 X의 결합 pdf와 ii) 확률 변수 X3에 대한 Marginal pdf이다.
그리고 X1, X2 X3의 확률 변수의 정의가 주어졌으므로 이를 통한 정보는 다음과 같다.
X2는 X1에 종속된다.(범위를 확인해라!), X3는 X2에 종속된다.

X3의 범위는 X2 확률 변수에 대해서만 영향을 받는다. X2가 주어진다면, X1과는 독립이다. 그렇기에 X3|X2의 조건부 PDF를 다음과 같이 표기할 수 있다. # 풀이 핵심1

# 풀이 핵심2: Joint(결합)는 Marginal(주변부) x Conditional(조건부) 를 이용한다.

우린 조건부 PDF를 알고 있다. 이 때, 결합 PDF를 알기 위해서 위와 같은 방법을 사용하면 된다.

ii) X3의 marginal pdf를 구하는건 매우 쉽다.. X1,X2,X3에 대한 결합 PDF를 구했으니 이를 X1, X2에 대해 전구간 연산하면 된다. # 이 때 적분 범위를 잘 생각해야한다. 각 X1, X2가 어떤 변수에 대해 제한되어 있는지 봐라 상수 범위가 아니다.

이 문제를 자주 풀자..
- 독립 ********

pdf가 확률변수 각각의 pdf의 곱으로 표현된다면, 각 확률 변수는 독립이다. 필요 충분조건이니까, 독립이면 각 pdf 곱으로 표현되고, 각 pdf의 곱으로 표현되면 독립임을 알 수 있는 것이다.
*** 관련된 중요한 성질 ***
# 같은 모집단에서 뽑은 샘플은 모집단의 분포를 따르는 확률 변수이고, 각각 독립이다.
그렇기에 위 독립 필요충분조건에 의해 각각의 pdf를 곱하여 결합 pdf를 구할 수 있다.

위 성질을 통해 모수를 추정한다.. 이게 뭔 소린지 꼭 이해하고 넘어가야 한다.

같은 모집단에서 뽑은 샘플 X1, X2, ... Xn은 각각 모집단의 분포를 따르는 확률 변수이다. (iid)
(여기서 모집단은 정규분포를 따른다고 본 것이다.)
또한 샘플을 뽑는 것은 독립이므로 각 확률 변수가 독립이라 아래를 성질을 만족한다. (독립의 필요충분조건 사용)

cf) 뽑은 샘플들은 뽑을 때 마다 달라질 것이니까.. 표본 평균 또한 확률 변수이다.
위 성질과 사전 지식을 사용하여 모수를 추정할 것이다. 예시를 통해 설명하겠다..
<Example>
우리는 모집단이 베르누이 분포를 따르는 것을 안다고 가정하자, 하지만 모수 p에 대해서는 알지 못한다.
더 쉽게 설명하면.. 베르누이 분포를 설명할 때 가장 자주 사용되는 동전 던지기라고 생각해보자. 분명히 동전 던지기를 하면 모수 p는 1/2가 나와야 하는데 이 동전이 휘어있는지 1/2가 나오지 않아.. 즉 모수를 모르는 거지.. 이 때 우리는 동전을 계속 던저보며 표본을 추출하고, 표본을 통해 모수를 추정할 거다.. 이에 대한 방식을 설명하고 있는 것이다.
(모수 p를 알기 위해 우리는 위 Likelihood를 사용하는 것이다. # 데이터로 부터 거꾸로 모수를 추정.)

모집단에서 크기가 10인 X1, X2, ... X10을 추출했다. X1, X2, ..X10은 모집단의 분포를 따를 것이다.
즉 X1, X2, ..X10은 p의 확률로 1의 값을 갖고, 1-p의 확률로 0의 값을 갖는 확률 변수이다.
이 때 X1 = 1, X2 = 1, X3 = 0... X10 = 1의 값을 갖는다고 해보자. (1이 6개, 0이 4개)
각 확률변수의 pdf는 다음과 같다.

이 때, 위 성질에 의해 같은 모집단에서 샘플링한 확률 변수는 독립의 필요 충분 조건을 만족하므로 결합 pdf를 구할 수 있다.

결합 pdf를 구하면서, 모수 p에 대한 함수가 나왔다. 이게 바로 Likelihood이다. Likelihood(p) = p^6(1-p)^4
이 함수가 최대값이 되는 p를 구하면 이게 바로 추정한 모수가 된다. # 내가 본 표본의 확률을 최대로 하는 p를 구하자.

결합 pdf는 내가 뽑은 샘플이 나오는 확률을 말한다. 즉 이 확률이 최대가 되는 p를 구해서 이를 모수로 추정하면 된다.
(likelihood를 미분해서 극대, 극소를 구하고, 구간 끝을 보면 되겠지..)
요약: 모수를 추정하기 위해 샘플링한 샘플들은 각각 모집단의 분포를 따르는 확률 변수이다. 또한 이 각 확률 변수는 독립이므로 결합 pdf를 구할 수 있다. 이 때 구한 결합 pdf가 Likelihood이다. 이 Likehood는 내가 샘플링한 데이터의 확률을 의미하며, 이 확률을 최대로 하는 모수를 구하여 이를 추정값으로 이용한다.
꼭 p가 아니라도.. 모집단이 정규 분포를 따르고, 모수인 평균을 모를 때 등.. 모든 경우에 사용할 수 있다.
<Example 6.8>
모집단이 정규분포를 N(0,1)을 따른다 하자. 위 성질에 의해 뽑은 X1, X2, X10의 결합 pdf는 다음과 같다.

걍 그렇군..
2. 확률변수들의 함수
- 순서 통계량

모집단에서 샘플링한 랜덤 표본 X1, X2, .. Xn을 작은 것 부터 크기 순으로 나열한게 바로 순서 통계량이다.
( )안에 들어가는게 순서이다.
- 순서 통계량의 PDF

<Example. 순서 통계량의 PDF 공식>
각각의 PDF의 곱 x n!를 하면 된다. # 정의역과 순서 통계량 언급을 꼭 해줘야한다.

- 순서 통계량의 Marginal PDF **공식 암기**


음.. 예시를 통해 확인하자.
<Example. 순서 통계량의 pdf #CDF를 구한 후 미분한다.>

일단, X1, X2, .. Xn은 지수 분포에서 뽑은 확률 변수이다. 당연히 독립이고, 지수분포를 따를 것이다.
이걸 작은 순서부터 나열하면 순서 통계량이 되고 가장 큰 값을 갖는 확률 변수가 X(n)이 될 것이다.
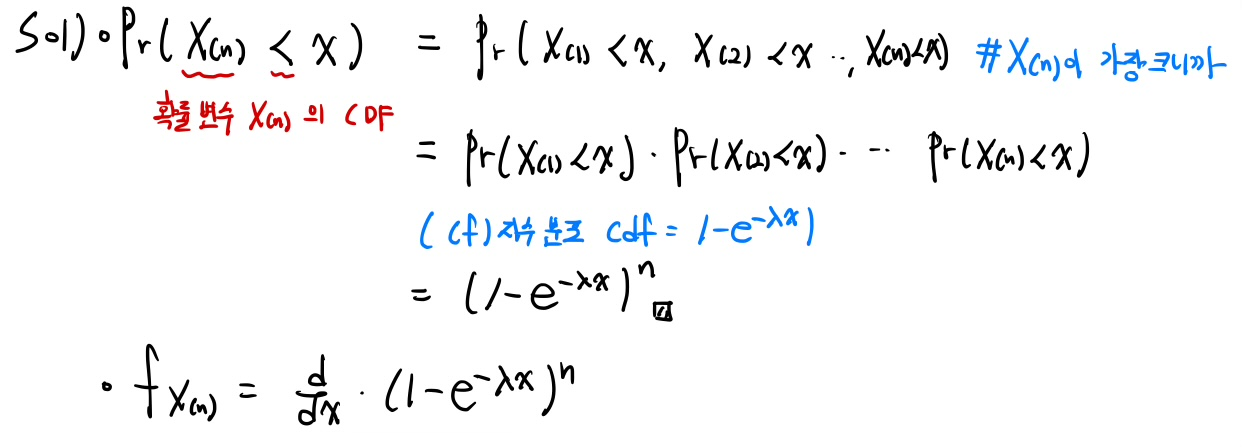
우선, 순서 통계량을 이용한다. X(n)이 x보다 작다는 것은, 모든 순서 통계량이 x 보다 작다는 것이다.
또한 순서 통계량은 지수 분포에서 샘플링한 확률 변수를 줄세운 것이므로.. 결국 얘도 독립이고, 확률 변수이다. 이를 이용해서 연산을 쉽게 해결한다. pdf는 그냥 cdf를 미분해서 구하면 된다.
** <Example 6.9> **

W는 X(n), Z는 X(1)임을 바로 알 수 있다. 순서 통계량 중 가장 큰 X(n)의 cdf, pdf는 위 예시처럼 그냥 풀면 된다.
하지만 가장 작은 X(1)은 여집합을 생각해서 풀어야한다.

Fz(z)의 CDF인 Pr(Z <z) = Pr(X(1) < z)는 여집합을 통해서 구한다.
이에 대한 여집합은 Pr(X(1) >= z)이고, 가장 작은 순서 통계량 X(1)이 x보다 크거나 같으므로, X(2), .. X(n) 또한 x보다 크거나 같을 것이다.
<Example 6.11>

지수 분포의 확률 변수의 의미는 첫 성공할 때 까지 걸리는 시간을 의미했다. 이 경우 첫 성공이 아닌 적어도 하나의 부분 시스템이 고장날 시간일 것이다. 순서 통계량 중 가장 큰 값은 가지는 X(n)이 최대 동작시간이 될 것이다.
(X(1) = 3 : 첫 번 째 고장 시간이 3.... 이렇게 생각해보면 X(n) 때는 마지막 고장 시간일 것이고, 이는 문제 설명에 의해 최대 동작 시간일 것이다.)
즉 우리는 X(n)의 cdf를 구하면 된다. 최대 순서 통계량의 cdf는 너무 너무 구하기 쉬웠다.

- 누적 분포 함수를 이용한 방법 (확률 변수의 함수 값을 확률 변수로 갖는 경우)
1) 이산형

이 파트는 그냥 문제를 풀어봐야 알 수 있다.
<Example. 이산형 확률변수의 함수로 구성된 확률 변수의 pdf>

그니까 확률 변수가, 다른 이산형 확률 변수의 함수로 구성되어 있는 거야..
이 경우에는 그냥 모든 경우를 다 생각해주면 된다. Y1는 0, 1, 2, Y2는 0, 1의 값을 가질 수 있겠지. 이 경우에 대한 확률을 구해줘. #이산형 확률변수의 PDF의 함수값은 확률이다.

그냥 차분하게 매칭하면 돼.. 경우의 수는 6개가 있겠고, 그 각 경우에 대한 확률을 구해줘.
2) 연속형

포인트는 P(g(X) <= y)에서 g의 역함수를 넘겨서, X에 대한 CDF로 만들어 주고, 이를 미분하는거야.

** <Example. 연속형 확률 변수의 함수로 구성된 확률 변수의 pdf> **


증요한건, 함수 e^-y/람다가.. 단조성을 가져야 한다.
- 확률 변수의 변수 변환 ********* pdf에서 변수 변환을 할 때, 자코비안을 곱해줘야 한다.


음 이것도 그냥 문제를 풀면서 익숙해지는 것이 좋다.
<Example. 확률 변수의 변수 변환>

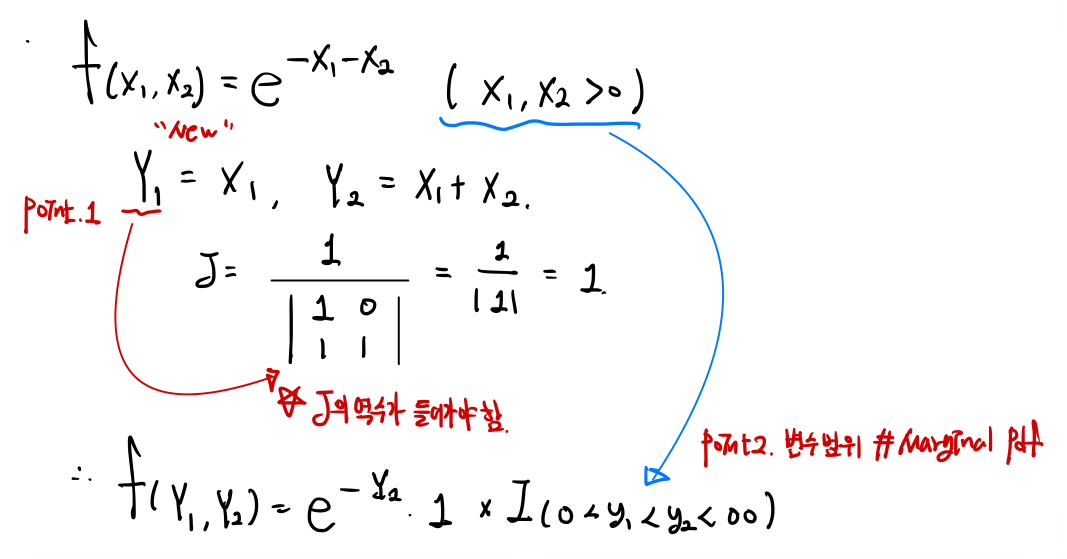
pdf에서 확률 변수 변환을 할 때, 자코비안을 곱해줘야 한다. 만약 위와 같이 새로운 변수를 기존 변수로 정의한다면, 자코비안의 역수를 곱해줘야 한다. 또한 확률 새로운 확률 변수의 범위를 꼭 잘 적어줘야한다.
새로운 확률 변수의 범위를 통해, Marginal pdf를 구할 수 있다.

*** <Example 6.14> ***

뭔가 확률 변수를 변환하고, 그 중 하나(V)의 pdf를 구하는 것이다. 즉 확률 변수 변환 후의, marginal pdf를 구하면 된다.
cf) 기존 확률 변수만큼 새로운 확률 변수가 필요하다. (변환하는 차원이 맞아야 하기 때문에)

정규 분포, 카이 분포의 pdf를 외우고 있어야 풀 수 있다... v, w의 결합 pdf를 구하고, v에 대한 marginal pdf를 구하면 된다.
교수님이 알려주신 카이 제곱 분포의 pdf가 조금 이상하다..

- 합성곱(Convolution) 형식 : 새로운 변수 Z에 대해, Z = X + Y로 변환될 때의 공식 (X, Y는 독립이어야한다.)

음 이게 뭔가 싶을 거다.. 만약에 이 공식이 없다면, 우선 X, Y를 변수변환 할 때, 차원을 맞추기 위해 새로운 변수를 정의해야 한다. 이에 대해 변수 변환을 마친 후, 또 Z에 대한 marginal pdf를 구해야 Z의 pdf를 구할 수 있다. 하지만 합성곱의 형태는 이러한 공식이 존재하여 쉽게 구할 수 있는 것이다.
# 합성곱 형태 변수 변환 공식 증명 *******
1) 확률은 기댓값으로 볼 수 있다.
2) 조건부 기댓값의 기댓값은 그냥 기댓값이다.
이 두 성질을 사용하여 한 식을 유도할 수 있다. 이 식을 통해 합성곱 형태 변수 변환 공식을 증명하겠다.

이 식을 사용하여, 합성곱 형태를 증명한다.

<Example. 합성곱 형태의 확률 변수의 변수 변환>

사실 간단한 문제는 이렇게 풀어도 되긴 한다.. 자코비안과 새 변수에 대한 정의역을 조심하면 그냥 풀 수 있다..
# 오답. 2번에서 아래처럼 바꿔야한다.. 그냥 합성곱으로 풀자...
공식을 적용한 풀이는 다음과 같다.

3. 기대값
4. 적률생성함수
는 다음 글에서 다룬다.
'학부 수업 > 확률 및 랜덤 프로세스' 카테고리의 다른 글
| ch7. Sum of Random Variables (0) | 2024.06.10 |
|---|---|
| ch6. Random Vector (2) (1) | 2024.06.05 |
| ch5. Pair Of RVs(2) - 이변량 정규분포 (0) | 2024.05.13 |
| ch5. Pair Of RVs (0) | 2024.05.09 |
| ch4-2. simulate RV (0) | 2024.05.09 |