서울시립대학교 인공지능학과 정지영 교수님의 패턴인식 강의를 정리함을 미리 알립니다.
<목차>
Continuous Time Convolution
Convolution Properties
The Response of LTI Systems to Complex Exponentials
CTFS
DTFS
L02에서 배운 LTI Convolution을 CT 신호에 대해 적용해볼 것이고, 푸리에 시리즈를 공부할 것이다.

- Continuous Time Convolution
L_02 DT 신호에 대한 LTI Convolution에 이어서 CT 신호에 대해서는 어떻게 될까? 를 공부할 것이다.
결론부터 말하자면, 모든 CT 신호도 Impulse 신호로 표현할 수 있으며, LTI 시스템이라면 Output를 합성곱을 통해 구할 수 있다.
우선 CT 신호를 Impulse 신호로 표현하는 방법에 대해 알아보겠다. 이 때, 다음과 같은 함수를 정의하고 사용해야한다.


해당 과정이 이해가지 않는다면, △의 범위를 잘 생각해보자. $X(0), X(△)..$ 에서 계속 1/△ 값을 줄 것이다. 이 때 크기를 1로 보정하기 위해 △를 다시 곱해줘야한다.

더 정확한 근사를 위해 △를 0으로 보낸다. 이 때 정의한 함수가 Impulse 신호가 된다. 이 과정을 통해 임의의 CT 신호를 Impulse 신호로 표현할 수 있었다. 이를 CT 신호의 Sifting property라고 부른다.
이렇게 바꾼 Input 신호를 LTI 시스템에 넣으면, 시스템의 특성에 의해 다음과 같이 Output을 매우 쉽게 계산할 수 있다.

△->0 일 때 정의한 함수가 Impulse 함수가 되며, 정의한 함수의 response가 Impulse response가 된다.
요약: 모든 CT 신호도 Impulse 신호로 표현할 수 있으며,
LTI 시스템에 이를 넣으면 합성곱 연산으로 쉽게 Output을 예측할 수 있다.
ex1) 유형: CT Convolution

so1)

Tip을 잘 확인하자. 이렇게 풀어야 안 헷갈리고 잘 풀 수 있다.
ex2) 유형: CT Convolution ****

sol) Tip 부분을 잘 보자!!

두 예제를 자주 풀어보자.
- Convolution Properties #교분 결
1) 교환 법칙 Commutative Property : 합성곱 순서 바꿔도 된다.
$X1 * X2 = X2 * X1$

2) 분배 법칙 Distributive Property, Parallel Systems: 분배해도 되고, 한 번에 넣어도 된다.
$X1*(X2 + X3) = X1*X2 + X1*X3$

3) 결합 법칙 Associative Property, Serial Systems # 이 법칙은 LTI Convoulution에서만 적용 가능하다. **o/x point
$X1*(X2*X3)$ = $(X1*X2)*X3$

선형 시스템이 아닌 경우, 이 4개가 동치가 아닐 수 있다. 결합하고 순서를 바꾸는 경우, 시스템이 선형 시스템이 아니면 결과가 다를 수 있기 때문이다. 상수배 한 후 제곱하는 것과, 제곱하고 상수배 하는 것은 다른 걸 예시로 들 수 있다.
+ System Inveribility *** 자주 회독. 헷갈림

이러한 시스템이 존재한다면, 두 Impulse response의 합성곱은 Impulse 신호가 나와야 한다. Q. O.X 포인트 성질 암기
아래 예시를 보면서 더 정확하게 이해해 보자.
ex1) Accumulator System
Impulse response가 step 신호인 DT LTI 시스템을 생각해보자.

임의의 Input 신호 X[n]에 대하여 다음과 같이 Impulse 신호로 표현할 수 있고, LTI 시스템이기에 합성곱으로 결과를 계산할 수 있다.

해당 시스템이 현재 Input 신호를 넣으면, 지금까지의 모든 Input 신호를 합쳐주는 시스템임을 파악할 수 있었다.
이에 대한 Inverse System을 생각해보자.
Inverse System은 input 신호로 y[n]을 받아, Output 신호로 현재의 Input 신호 X[n]을 뱉어야한다.
즉 Inverse System Z[n]은 다음과 같이 정의할 수 있다.
$$Z[n] = y[n] - y[n-1]$$
자! System과 Inverse System을 얻었다. 두 시스템에 대한 Impulse Response의 합성곱은 Impulse 신호가 나오는지 확인해보겠다.
기존 시스템의 Impulse Response는 문제에서 u[n]으로 주어졌다.

Inverse System의 Impulse Response를 구하기 위해 해당 시스템에 Impulse 신호를 Input으로 넣으면 다음과 같이 구할 수 있다.
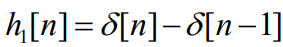
두 Impulse response를 합성곱 해보겠다.
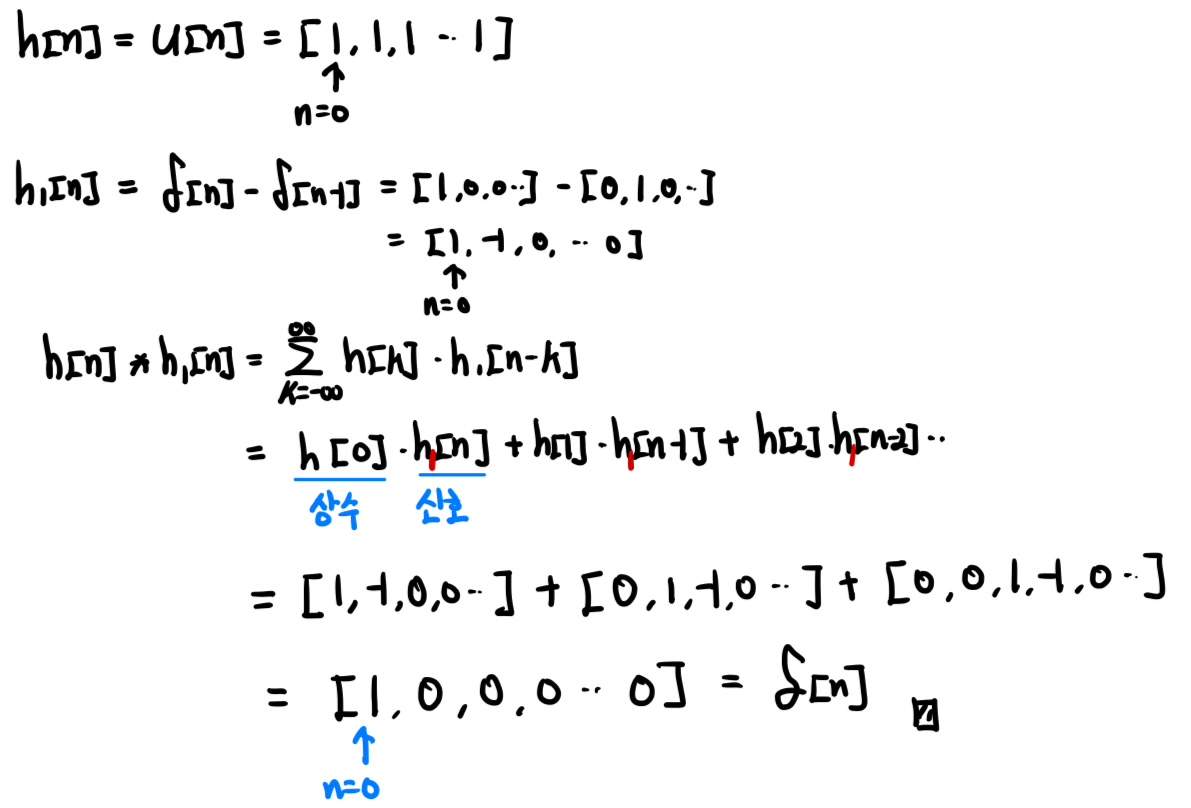
시스템과 역 시스템의 각 Impulse response를 합성곱 해서 Impulse 신호가 나옴을 보였다.
- The Response of LTI Systems to Complex Exponentials
지금까지, 모든 CT, DT 신호는 Impulse들의 가중치 합으로 표현할 수 있고, 이를 LTI 시스템에 넣는다면 시스템의 특성 때문에 합성곱 계산으로 쉽게 Output을 계산할 수 있다!! 를 공부했다.
여기서는 신호가 '어떤 특정한 모양'을 가질 때, 계산이 간단해지는 것을 공부할 것이다.
LTI System에 들어갈 Input이 다음과 같이 복소 지수 Complex Exponentials 형태이면, 같은 complex exponential에 크기만 변한 형태로 Output 신호가 나온다. # 진폭만 변화하고, 같은 복소지수를 갖는다.

어디서 많이 본 듯하다. 복소 지수 형태의 Input 신호는 고유 벡터이고, 크기를 바꾸는 H는 고유치라고 생각하면 쉽다!
이를 증명해보겠다. **시험 대비**


h(s)만 계산할 수 있으면 시스템의 아웃풋을 편하게 구할 수 있다. 다음 같이 활용할 수 있다.

>> 쪼갠 복소 지수 계수, 고유 값, 고유 벡터의 가중치 합으로 쉽게 아웃풋을 구할 수 있다.
cf. 연속 및 이산시간에 대하여 LTI 시스템의 입력이 복소지수의 선형결합으로 표현된다면, 출력 또한 같은 복소지수신호의 선형 결합으로 표현될 수 있다는 것이다. 이래서 아웃풋 신호 예측이 쉽다는 것이다.
ex1) 유형: Input이 복소 지수 형태인 경우, LTI System의 Output 구하기.

Impulse Response가 주어져있기에, 그냥 뇌 빼고 X(t)를 Impulse 신호 형태로 바꿔서, 합성곱을 통해 Output 신호를 뽑아내도 된다. 하지만, 이 문제에서는 Input이 복소 지수 형태인 것이 포인트다. 이를 잘 활용해보자.

그래.. 이렇게 Input이 복소 지수 형태, 즉 Complex Exponentials로 이루어져있으면 계산이 쉽다는 것을 알 수 있었다.
그러면.. 여기서도 똑같이 모든 신호를 Complex Exponentials 신호들의 합으로 표현할 수 없을까? 를 고민하게 된다.
cf. 앞에서 모든 신호를 Impulse 신호 합으로 표현했었다. 이렇게 한 번 복소 지수 형태로 해보자는 것이다.
cf2. 특정 신호들은 복소 지수 형태의 신호들의 합으로 표현할 수 있다. 이 때 사용되는 게 바로 푸리에 시리즈이다.
>> 바로 다음 글에서 배울 것이다.
https://dogunkim.tistory.com/56
PR_L03. Fourier Series ((2))
보호되어 있는 글입니다. 내용을 보시려면 비밀번호를 입력하세요.
dogunkim.tistory.com
'학부 수업' 카테고리의 다른 글
| 자연어처리 중간고사 문제 풀이 (1) | 2024.11.05 |
|---|---|
| PR_L03. Fourier Series ((2)) (1) | 2024.10.16 |
| PR_L02. Signals and Systems (1) | 2024.10.14 |
| Introduction to RL (week 1) (3) | 2024.09.23 |