Ch 02. Point Cloud Processing Backbone
<목차>
2-1. PointNet
2-2. PointNet++
2-3. Graph Convolutional Network
2-4. Dynamic Graph CNN
2-5. Kernel Point Convolution
https://arxiv.org/abs/1801.07829
Dynamic Graph CNN for Learning on Point Clouds
Point clouds provide a flexible geometric representation suitable for countless applications in computer graphics; they also comprise the raw output of most 3D data acquisition devices. While hand-designed features on point clouds have long been proposed i
arxiv.org
2-4. Dynamic Graph CNN(DGCNN)
앞서 공부하며 Point cloud는 비정형 데이터라 슬라이딩 윈도우 방식의 CNN을 사용하기에는 한계가 있다고 언급했다.
이 한계를 극복하려고 한 논문이 바로 Dynamic Graph CNN 논문이다. Point cloud에 CNN 구조 자체를 사용하려는 연구를 보였다. 이에 대해 공부해보자.
cf. PointNet++ 에서도 CNN 같은 컨셉으로 local feature를 학습시키려고 했다.
- DGCNN Main contributions
Point cloud를 위한 딥러닝 구조인 PointNet 그리고 일반화된 구조에서 Convolution 연산을 할 수 있는 GCN을 결합하여 활용하자고 시작한 것이 바로 DGCNN이다. PointNet++ 처럼 local geometric structure을 기반으로 특징 학습에 접근하고, 이를 구성함에 있어서 point들을 그래프로 묶어 local 구조를 학습한다는 것이 핵심이 된다.
- DGCNN architecture

- Edge Convolution

함수를 설정해 우리는 원하는 feature를 도출한다고 해보자. 우리는 i 노드의 feature $x_i$와 주변 노드 feature인 $x'_j$을 통해 원하는 feature인 $x'_i$를 도출해야 한다. 이를 위해 논문에서는 symmetric aggregation operation ㅁ과 edge features를 뽑아내는 비선형 함수 $h_Θ$를 결정해야 한다 말한다. 이 때 이 비선형 함수는 학습 가능한 parameter Θ를 포함한다. 이 함수를 결정하기 위한 시도들은 다음과 같았다.
- 1) i와 인접 j 포인트들에 대한 단순 컨볼루션 연산

2차원에서 i라는 pixel과 커널 사이즈에 해당하는 j라는 픽셀에 연산을 시도. 구조적인 한계 때문에 적용할 수 없었다.
- 2) PointNet

PointNet이기에 global shape의 feature만 뽑아내는 한계를 가졌다.
cf. PointNet++ 에서 PointNet은 local feature를 잘 뽑아내지 못한다고 언급.
- 3) Gaussian kernel과 pairwise distance를 활용

함수 u 를 사용하여 pairwise distance 계산. 이에 gaussian kernel를 적용한 결과값을 feature를 뽑을 때 사용함.
인접한 point에 대해서 적용하다보니 local 정보를 뽑기에는 좋았지만 global structure를 보기에는 어려움이 있었다.
- 4) 상대 거리를 입력으로 사용

동일한 구조지만, i와 j의 상대 거리를 사용했다. PointNet에서 보이듯이 이렇게 상대 거리를 사용하면 local feature를 뽑아내는 데 좋은 효과를 보인다. cf. 상대 거리를 사용하면 point to point의 관계 측면에서 feature를 잘 잡음.
하지만 global shape structure를 잘 캐치하지 못했다.
그렇다면 위에서 사용된 global shape feature를 잘 파악하는 2번과 local feature를 잘 뽑은 4번을 조합하는 건 어떨까?
- 5) i의 절대적 위치와 이웃 포인트의 상대거리를 모두 입력으로 사용

해당 논문에서는 전처리 과정을 하지 않고 PointNet 처럼 그냥 사용하도록 절대적 위치인 $x_i$, 그리고 상대적 거리인 &x_j - x_i&를 모두 사용하여 global, local feature를 잘 포착할 수 있었다.
- Edge Convolution architecture

절대적 위치인 $x_i$, 상대적 거리인 &x_j - x_i&를 입력으로 받아서 edge features를 도출하는 비선형 함수 $h_Θ$에 집어 넣는다. 이후 symmetric aggregation operation인 Max Pooling을 통해 원하는 feature $x'_i$를 도출해낸다.

cf. $h_Θ$는 MLP로 구현된다.
- Dynamic graph update
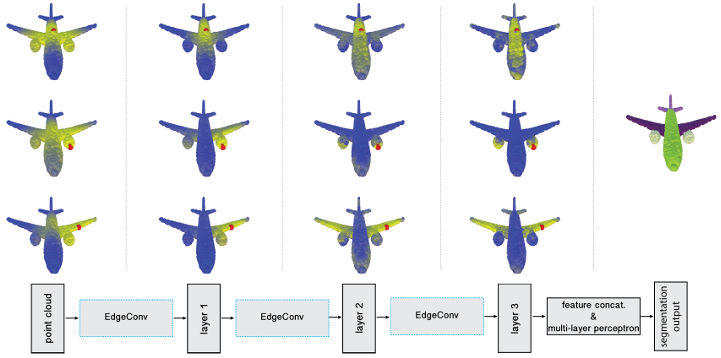
Dynamic graph의 영역 자체는 매 레이어마다 연결 관계성을 다시 한 번 점검된다. 연결성은 고정되어 있지 않고 매번 네트워크를 학습할 때마다 이번 에폭에서는 어떻게 연결되어 있는게 효율적이었네? 학습, 반복하며 최적의 연결성을 찾아 Graph를 업데이트한다.

3번 째 열 예시를 봐보자. 처음에는 물리적인 거리에 집중하여 연결 관계성을 가져 반대 날개를 날개라고 구분하지 못하고 있지만 레이어를 거치며 점점 의미론적으로 비슷한 곳에 연결 관계성을 보이며 semantic segmentation을 잘 해내고 있다. cf. 빨간색 점이 내가 구분하고자 하는 것이다.
- Properties of DGCNN
- 1) Permutation invariance**: 순서 불변성... 입력 벡터 요소 순서와 상관 없이 같은 출력을 생성하는 모델
Symmetric function(Max pooling)을 사용하면서 해당 조건을 만족할 수 있었음.
-2) Translation invariance**: input의 위치가 달라져도 동일한 값의 output 을 생성하는 모델.
상대 거리 입력이 둘 간의 상대 정보이기 때문에 부분적으로 해당 조건을 만족할 수 있음. 둘 간의 상대 거리는 변하지 않음
위 DGCNN의 두 속성은 Point cloud의 특성을 생각해보면 쉽게 이해할 수 있다.
- Experiments
- Classification

타 모델 대비 높은 성능의 정확도 보임 Overall accuracy가 가장 높음
- 효율성

작은 용량으로 좋은 연산 시간과 성능을 보인다.
- 추가 실험


서로 다른 성분을 썼을 때의 결과 비교, 이웃 포인트 개수 설정에 따른 실험 결과 비교
- 파트 분할 결과


PointNet대비 식별 오차 적음. + 좋은 컴퓨팅 성능을 보임.
- Semantic segmentation 결과 비교

PointNet 대비 식별 오차 적음
cf. 좀 많이 빈약하게 이해한 논문 같다.... 어느 정도 경험치가 더 쌓이면 Edge Convolutuon 부분쪽으로 다시 공부해보자....
symmetric aggregation operation
edge features
Gaussian kernel
2-5. Kernel Point Convolution
'Autonomous Driving > 2. LiDAR Perception' 카테고리의 다른 글
| Ch03. Point cloud matching - 1) point cloud 매칭 및 활용 분야 (0) | 2024.09.12 |
|---|---|
| Ch02. Point Cloud Processing Backbone - 5) Kernel Point Convolution (0) | 2024.09.10 |
| Ch02. Point Cloud Processing Backbone - 3) Graph Convolutional Network(GCN) (1) | 2024.09.09 |
| Ch02. Point Cloud Processing Backbone - 2) PointNet++ (0) | 2024.09.06 |
| Ch02. Point Cloud Processing Backbone - 1) PointNet (2) | 2024.09.06 |