서울시립대학교 인공지능학과 정지영 교수님의 컴퓨터 비전 개론 수업을 정리함을 미리 알립니다.
- Contents
렌즈를 장착한 카메라들에 대해 알아볼 것이다.
1. Pinhole Model
2. Thin Lens Law
3. Lens Properties
4. New Types of Cameras
- Pinhole Model (3−1)
1. 핀홀의 존재 이유

핀홀 카메라에서 핀홀이 있어야하는 이유가 뭘까? 바로 광 다발을 포착하기 위해서이다. 핀홀이 없으면 이러한 광다발을 잡지 못하고, 빛이 여러 곳에 도착하여 정확한 상이 맺히지 않는다.
핀홀 카메라에서는 이 핀홀이 바로 center of projection focalpoint이다.
2. 핀홀의 크기
그러면 이러한 핀홀의 크기는 어떻게 하는게 좋을까?


1) 핀홀 크기가 너무 크면, 많은 방향의 광선이 평균화되어 흐려진다.
2) 핀홀 크기가 너무 작으면, '회절 효과'로 인해 이미지가 흐려진다. 물론 어두워지기도 한다.

-> 그렇기에 너무 크지도, 작지도 않은 적당한 핀홀 크기가 필요하다.
이러한 핀홀 사이즈를 조절해도 일반적으로 너무 어두워서 사용하지 않는다. 광선만이 스크린에 도달하기 때문이다.
-> 핀홀 카메라의 절대적인 광량의 부족으로 렌즈가 도입되게 된다. 렌즈를 통해 빛을 잘 모아서 밝은 사진을 찍을 수 있게 된다.
CF. 셔터를 오려 열어둬서 억지로 밝게 만들 수는 있다. 하지만 정말 오래 열어둬야한다..
- Thin Lens Law (3−2)
렌즈를 도입하므로써 빛들이 잘 모여 짧은 셔터 시간으로도 충분히 밝은 사진을 찍을 수 있게 되었다.
1. 렌즈의 주요 속성
이러한 렌즈는 두 가지의 중요한 속성을 가진다.


속성1. 렌즈의 중심을 지나는 빛은 꺾이지 않는다.
속성2. 렌즈의 Optical Axis와 평행한 빛은 렌즈를 통과하면 '한 점'으로 모인다. 이 점이 바로 Focal Point이다.
2. 렌즈의 구성 요소

1) Optical Axis
-> 렌즈의 중심 Optical center(COP)를 지나며, 렌즈와 수직인 가상의 직선이다. 이 옵티컬 축과 평행한 빛들은 Focal Point에 생기게 된다. 이 축이 센서 플레인에 수직하게 잘 맞는다면 Skewness를 고려하지 않아도 되었다.
2) Focal Point
-> Optical Axis에 평행한 광선들이 렌즈를 통과하여 모이는 하나의 점.
3) Focal Length f # 렌즈의 고정 값
-> 위 Focal Point와 렌즈 사이의 거리이다.
4) Aperture # 조리개
-> 렌즈의 크기와 별도로 빛이 통과하는 구멍의 크기. 광량을 조절하게 된다. 지름을 구경(D)이라고 한다.
이걸 공부하면서 한 가지 의문이 생겼다. 아니 그냥 결국 Focal point를 포함해서 이미지 플레인 그니까 센서 플레인을 거기다가 두면 그냥 다 좋은거 아닌가? 왜 아래 Thin Lens Law 같은게 나온거지? 싶었다. ㅇㅇ 아니었다.
-> 모든 빛은 옵티컬 축과 평행하게 들어오지 않는다. 그렇기에 포컬 포인트에 이미지 플레인을 두게되면 엄청 멀리 있어서 빛이 거의 평행하게 들어오는 애들만 상이 잘 맞고 나머지는 잘 안맞을 것이다.
-> 즉 우리는 특정 물체를 찍고싶다!! 그러면 그 물체에 맞게 이미지 플레인을 둬야하는 것이다. # Thin Lens Law!!!!!!!
3. Thin Lens Law # 상이 잘 맺히는 위치 찾기 # 렌즈와 물체 거리, 초점 거리 f는 고정 # In-focus로 찍혔을 때


그니까 내가 찍고 싶은 물체는 D 거리에 있고 이는 고정이다. 또한 내 렌즈는 하나라 초점 거리 f도 고정이다.
-> 이 때 어디다가 이미지 플레인를 둬야 상이 잘 맞지? 를 계산할 수 있는 공식이 되겠다.
4. Out-of-focus # DoF

이 상황은 빛이 평행하게 들어와서 D' = f 인 상황이다. 이 때 D'과 비슷하게 이미지 플레인을 두면 이를 In-focus라고 한다.
해당 위치에 비슷하지 않게 이미지 플레인을 두면 Out-of-focus가 발생한다.
cf. 물체의 빛이 평행하게 들어온다 = 엄청 멀리 있어서 빛의 벡터가 거의 평행하다...
이렇게 D' 주변에 상이 잘 맺히는 부분을 Depth of Field(DoF)라고 한다.

DoF는 Aperture 즉 조리개를 조절하여 바꿀 수 있다. 이걸 조절하면 초점이 안맞는 물체들를 In-Focus로 만들 수 있다.
어? DoF가 넓으면 다양한 거리에 있는 많은 물체들이 초점이 맞을 텐데 그러면 무조건 구경은 작은게 정답인가?
-> ㄴㄴ 아니다. 구경이 작아지면 들어오는 빛의 양이 줄어들고, 어두운 사진이 된다. 그렇기에 셔터를 오래 열어둬야하는데 이러면 물체가 흔들리거나 했을 때의 노이즈에 민감하게 된다. 번진 사진이 나온다.
이러한 빛의 양을 나타내는 F넘버를 알아보자.
5. F/Number # 빛의 양을 일정한 수로 나타내는 것


이게 처음 보면 좀 헷갈리는게 f/숫자 이렇게 표현해서 뭐 나누기인가.. 저기에 구경 D가 들어가나? 어지럽다.
-> f/d를 먼저 계산하고 이 결과를 f/결과 << 이렇게 표기하는 것이다. 나누기가 아니다.. 그냥 노테이션이 이렇다.
ex) 초점 거리 3, 구경 2 -> f/3/2 = f/1.5
이를 해석할 때는 분자 f를 고정하고 생각해보자.
Q. f/1 vs f/22 뭐가 더 밝은가?
> 이걸 일단 나누기로 생각하면 안되는건 위에서 설명했다. 1 vs 22로 놓고 생각하자.
>> f/d를 했을 때, f가 고정이라고 했을 때, 22가 d가 더 작을 것이다.
>>> f/22가 더 어두운 렌즈이다.


6. Field of View (FoV)
얼마나 많은 넓은 시아각을 찍을 수 있냐의 메트릭이다. DoF랑 헷갈릴 수 있다 ㅇㅇ.. 완전히 다른 거다.

Focal Length ↑ = 줌 ↑ = 시야각 ↓
당연하지만 단 렌즈는 초점 거리를 조절할 수 없다. 렌즈를 바꾸거나, 여러 개를 껴서 간격을 조절하거나.. 해야한다.
Lens Properties (3−3)
1. Lens Glare
-> 렌즈 내부의 빛 반사로 인해, 아주 밝은 광원이 있을 때 생기는 빛 번짐

2. Chromatic Aberration, 색 수차
-> 렌즈는 파장에 따라 서로 다른 굴절률을 가지기에 생기는 빛 번짐

물리 법칙에 의해 일어나지만, 렌즈를 잘못 깎으면 더 심해진다.
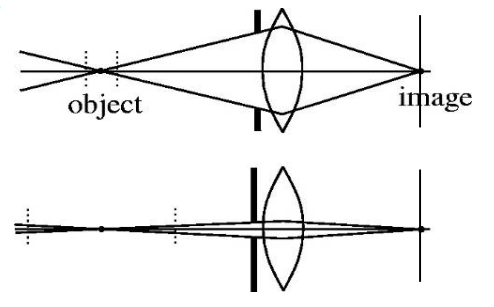
3. Vignetting, 비네팅
-> 렌즈를 여러개 썼을 때, 옵티컬 축에 가까운 물체들의 빛이 더 많이 들어오고 멀어질 수록 빛이 덜 들어오는 현상


렌즈를 잘못 깎아서라기 보다는, 렌즈를 여러개 써서 그렇다. 위 그림을 보면 쉽게 이해할 수 있다.
4. Spherical aberration, 구면 수차 # 렌즈를 잘 못 깎아서 생기는 문제
-> 옵티컬 축과 평행하는 빛이 한 점이 모이지 않는 현상. 광축에서 멀어질 수록 더 가까운 곳에 모인다.

5. Radial Distortion # 렌즈를 완전하게 만들 순 없기에..
-> 중앙에서 멀어질 수록 왜곡이 심해짐. 더 많은 면을 보기 위해서 광각 렌즈 쓰면 이러한 왜곡이 발생한다.

| 1 | Lens Glare | 렌즈 내부 빛 반사 | 아주 밝은 광원이 있을 때 렌즈 내부 반사로 생기는 빛 번짐 |
| 2 | Chromatic Aberration 색 수차 | 파장별 굴절률 차이 + 렌즈 제작 미세 오류 | 렌즈가 파장에 따라 다른 굴절률을 가지면서 색 번짐 발생, 렌즈를 잘못 깎으면 더 심해짐 |
| 3 | Vignetting 비네팅 | 렌즈 복합 설계여러렌즈사용 | 광축에 가까운 빛은 많이 통과하고, 주변부는 적게 통과하여 이미지 가장자리가 어두워짐 |
| 4 | Spherical Aberration 구면 수차 | 렌즈를 이상적으로 깎지 못함 | 광축과 평행한 빛조차 한 점에 모이지 않고, 광축에서 멀수록 초점이 가까워지는 문제 |
| 5 | Radial Distortion | 렌즈 제작상 완전한 형태 불가 | 중앙에서 멀어질수록 왜곡이 심해지며, 광각 렌즈 사용 시 더 뚜렷하게 나타남 |
- New Types of Cameras (3−4)
1. Digital Camera
-> 필름 말고, 센서 배열에 이미지를 투영하는 카메라이다.

다음과 같은 두 과정을 따른다.1) Sampling: 어떤 픽셀을 사용할 건지 말지를 결정하는.. location(x,y)2) Quantization: 샘플링된 픽셀 전기 신호를 정해진 세기 레벨로 양자화하는 과정을 거친다.
픽셀 세기는 다음과 같은 2차원 함수로 표현하며, 만약 RGB 이미지면 3차원 벡터일 것이다.

만약 비디오라면 프레임 시퀀스 타임이 추가된다.
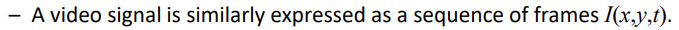
2. 360 cameras

3. Multi-spectral cameras

4. Light-field camera

5. Event camera

'학부 수업 > 컴퓨터비전' 카테고리의 다른 글
| 4. Projective Geometry 2 | 2025.04.22 |
|---|---|
| 2. Image Formation 2 | 2025.04.22 |