2. Image Formation

서울시립대학교 인공지능학과 정지영 교수님의 컴퓨터 비전 개론 수업을 정리함을 미리 알립니다.

• Contents

1. 3D to 2D projections

2. Photometric image formations

3. Digital cameras

 

 

• 3D to 2D projections $(2-1$)

1. Homogeneous Coordinates

 행렬 계산 편의 및 선형 시스템으로 정사영 시스템을 구성하기 위해서 다음과 같은 Homogeneous coordinates를 사용하게 된다.

 사용 방법은 간단하다. 차원을 하나 더 추가해주고, 이 성분을 1로 설정하면 된다. Euclidean 좌표계로 다시 돌아갈 때는 추가했을 때의 과정을 거꾸로 하여 마지막 좌표를 1로 만들어주고 마지막 차원을 제거하면 된다.

 

 

2. 3D to 2D projections

 사영에 대해 살펴보기 전에 우선 어떤 종류의 사영이 있는지 먼저 알아볼 것이다. 사영은 Orthography 그리고 Perspective Projection 크게 두 개로 나눌 수 있다.

 

1) Orthography Projection

 3차원 좌표의 z 성분을 단순히 제거하는 투영 방식. 긴 초점 거리 렌즈, 카메라와 객체 거리 대비 깊이 변화가 얕은 객체에 대한 근사 모델이다.

 

즉 3D의 x, y, z 성분 중에서 x, y 성분만 가져오고, z성분은 버리는 사영이 Orthography Projection이다. 행렬은 다음과 같다.

 틸다가 붙은 노테이션이 Homogenous 좌표계로 표현한 좌표이다. 행렬 계산을 해보면 x, y좌표는 그대로 오게 되고, 위에서 노란 부분의 성분이 0이기 때문에 z성분은 죽게 된다.

 

 만약 z성분을 죽이는 Orthography Projection을 하면서도 x, y 스케일을 조정하고 싶으면 Scaled Orthography Projection을 사용하면 된다. 

스케일을 추가한 직교 사영

 

2) Perspective Projection

 Perspective가 붙으면 z 값 즉 깊이에 따라 x, y 성분이 영향을 받는 걸 의미한다. 

 

 먼저 Perspective Projection이 있다. 대부분의 카메라는 다 이걸 따르게 된다.

직교 사영과 달리 3행 3열 위치에 0이 아닌 성분이 들어가게 된다. 이로 인해 z값이 계산이 되고 homo 좌표계를 유클리언 좌표계로 돌리는 과정에서 z값에 따라서 x, y 성분이 영향을 받게 된다.

 

 

 먼저 Para-perspective가 있다.

 

 두 Perspective Projection에 대해서는 4장에서 더 자세하게 배운다. 아 이런게 있구나. z성분이 아무것도 안하고 사라지던 직교 사영과 달리 Perspective가 붙은 사영들은 z 성분이 사영을 했을 때의 x, y 성분에 영향을 주는구나! 이해하고 넘어가면 된다.

 

 

 3. Pinhole Camera Model #K[R|T]

 핀홀 카메라 그리고 이를 모델링하는 행렬에 대해 알아볼 것이다. 간단하게 아 그렇구나! 하고 넘어가면 된다. 3, 4, 5장에서 더 자세하게 다룰 것이다. 3, 4, 5장을 공부하고 나서 되돌아와서 아 여기는 그냥 가볍게 이야기 한거구나 ㅇㅇ.. 하고 한 번 쓱 보면된다.

 

1) calibration matrix

 위에서 카메라의 사영 시스템 perspective 사영을 봤다. 이 때 원소들이 1 값을 가졌는데 그건 가장 간단한 형태이다. 사실 일반적으로는 렌즈의 초점 거리 포컬 랭스를 곱해 스케일을 조정해줘야한다.  

  또한 사영된 이미지의 좌표 원점을 가장자리 좌하단을 $0, 0$으로 지정하고 이를 기준으로 광축을 지나는 점 P 즉 '이미지의 중심'의 좌표 px, py를 표현해주면 다음과 같다.

cf. 이미지 중심 <-> 이미지 원점 ㅇㅇ.. 이미지 원점을 설정하고 중심을 알려주는 느낌이다.

 이걸 다시 K[I |O] 형태로 바꾼 다음에 K만 때서 보면 다음과 같다. 이를 calibration matrix라고 부른다.

 여기까지가 K[I |O]다. 사실 K 행렬은 

 

 

2) Camera rotation and translation

 카메라 기준 좌표계와 World 좌표계가 다를 수 있다. 그러므로 우리는 3D를 2D로 사영하기 전 해당 좌표계를 맞춰줘야한다. 우리는 World coordinates를 카메라 좌표계로 바꾼다. 뭐를 어떤 기준으로 바꾸는지 잘 생각하자.

ex) 카메라가 여러 대 있을 때.

O: World Coordinates/ C: Camera Coordinate system

 두 좌표계는 위치가 다를 것이고, 축이 다를 것이다. 이를 맞춰주기 위한 것이 바로 rotation and translation이다. 

 

 카메라 기준 좌표계에서 World 좌표계 방향으로의 벡터를 C라고 하자. 세계 좌표계에서 카메라 좌표계로 바꾸려면 우선 translation 즉 해당 벡터를 빼주면 된다. 이를 행렬로 표현하면 1번 과정이다. 이동 후 회전을 추가하면 좌표계를 맞춰주는 행렬 [R|T]가 완성된다. 참고로 회전 행렬은 roll, yaw, pitch 순서로 곱해줘야하는데, 이는 3,4 장에서 더 자세하게 다룬다.

벡터 방향을 헷갈리지 말자..

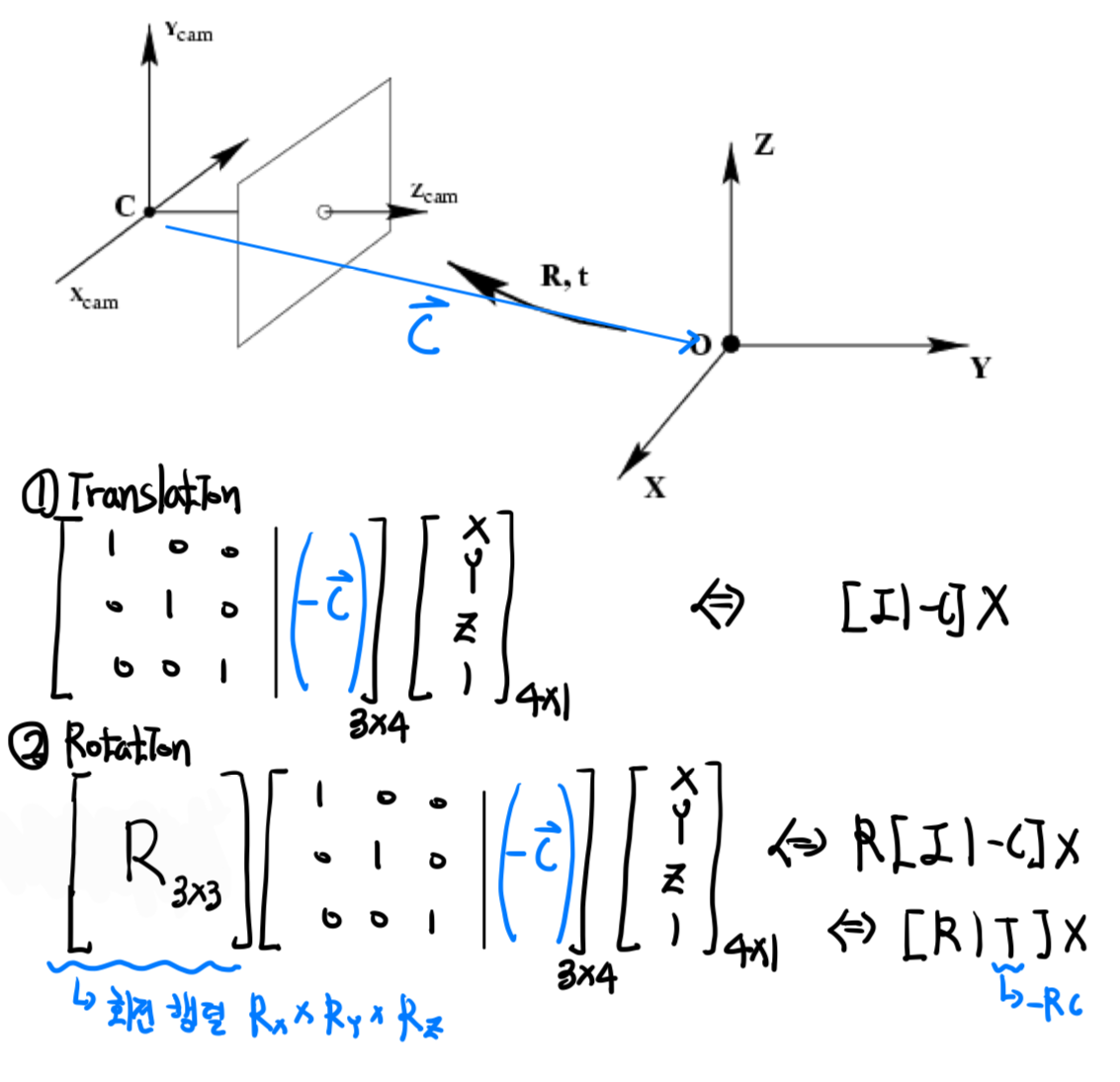
 캘리브레이션 행렬 K와 좌표계를 맞추기 위한 행렬 [R|T]를 알아보았다. 이제 최종적으로 3D 물체를 좌표계를 맞추고 + 3D -> 2D 사영을 해주는 계산은 다음과 같을 것이다. 만약에 카메라 기준 좌표계와 세계 좌표계가 같다면 [R|T] = [I|O]일 것이다.

Xcam은 카메라 좌표계로 바꾼 X를 의미한다.

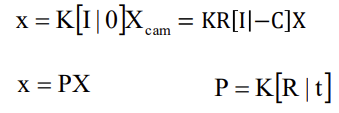
# 주의
여러 자료에서 가져오신 듯 하다.. 이 최종 행렬은 P 혹은 M으도로 표기한다.

[R|T] = R[I | -C] 행렬에 관련해서 T = -RC임을 꼭 알고 있자. T가 그냥 평행이동 벡터 아니야? 라고 생각하기 쉽다.

 

 Skew는 센서가 광축$optical axis$에 수직으로 장착되지 않았을 때 발생하는 왜곡을 의미한다. 이를 보정하기 위해서 켈리브레이션 행렬 K에 매개변수를 추가할 수 있다.

 

 사영된 이미지의 중심 Image center는 principal point라고 부르며 optical axis과 이미지 평면이 직교하며 만나는 지점이다. 

 

 

---

• Photometric image formations# 광학적 기반의 이미지 형성 $(2-2$)

1. Lens distortions

 3D를 2D로 바꾸는 행렬 계산은 리니어했다... 하지만 직선이 곡선으로 생기는 경우가 존재한다. 이는 렌즈에 의한 왜곡이다. 이러한 왜곡 종류 중 하나인 Radial distortions에 대해 간단하게 알아보자.

 

 광각 렌즈같은 걸 사용하면 아래와 같이 왜곡이 발생한다. 이미지의 중심점 Cx, Cy에서 멀어질 수록 왜곡이 심해진다. 이게 바로 Radial distortions이다.

술통 같이 생겨서 배럴이다..

  이를 보정하려면 다항식을 설정하고, 이를 잘 보정하는 parameter k를 구하면 된다. x^2 = $Cx - x$^2으로 이해하면 된다. 즉 아래 식은 멀리 떨어져있을 수록 보정을 많이 해준다는 뜻이다.

적당히 파라미터 1개정도만 구하는 모델링 하면 대충 잘 보정된다 ㅇㅇ..

펴다보니까 찍힌 내용이 없는 부분도 생긴다 사진은 네모 모양이어야 하니까 ㅇㅇ...

 보통 3D 재복원 분야에서는 이걸 이렇게 펼쳐서 사용한다.

 

2. Photometric image formation # 기말고사 범위 그냥 개념만 알고 넘어가자.

1) 이미지가 존재하려면....

이러한 광량을 더 잘 모으기 위해 핀홀말고 렌즈를 쓴다..

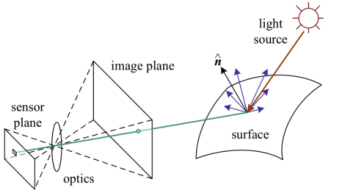
 빛은 광원 Light source에서 방출되어 물체의 표면에 반사된다. 이 중 일부 빛은 카메라를 향해 전달되어 상을 맺을 것이다. 단순화된 모델에서는 여러 번의 반사 현상은 고려하지 않는다.

 

 빛이 없으면 이미지는 존재할 수 없다. 이미지를 생성하기 위해서는 장면이 하나 이상의 광원으로 조명되어야 한다.

 

 이러한 광원은 점 광원인 경우 L$λ$로 모델링하며, 보다 복잡한 광원은 L$v,x$로 모델링, Environment map으로 표현한다. 

Environment map

2) Reflectance and shading

 빛이 물체 표면에 닿으면, 빛은 흩어지고 반사된다. 이는 빛마다 다른 특성을 갖는다.

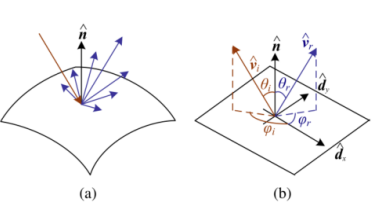
이 상호작용을 설명하기 위해 다양한 모델들이 개발되었다. 일반적인 형태로는 DRDF가 있으며, 특수한 모델로는 diffuse, specular, Phong model.. 등이 있다. 그냥 이런게 있구나~ 하고 넘어가면 된다. 나중에 더 자세하게 배울 것이다.

Bidirectional reflectance distribution function $BRDF$

Diffuse reflection: 난반사

Specular reflection: 거울과 같은 정반사

 

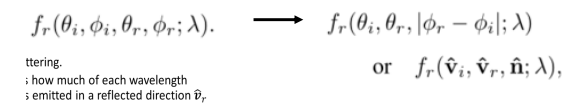
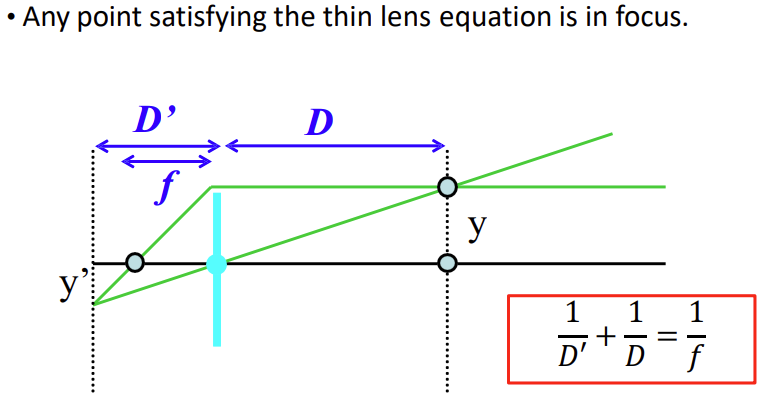
3) Thin lens law ***

 D′는 렌즈와 이미지 평면 즉 센서 사이 거리, D는 렌즈와 물체와의 거리이다. 이를 알ㅇ면 초점 거리 f를 구할 수 있다. 이 공식이 바로 Thin lens law이다. 3장에서 한 번 더 나올 것이다.

도형의 닮음으로 유도할 수 있다. 유도는 생략한다.

 

 

• Digital cameras $(2-3$)

렌즈 -> 구경 -> 셔터 -> 센서...