Data Compression 3

https://dogunkim.tistory.com/92

5. Data Compression 2

 

> 요약1) 정보량 공부

 모든 사건에 대하여 정보를 구분해서 기록하거나 보내기 위한 평균 비트 수 = 얻는 평균 정보량이 바로 샤먼 엔트로피다. 

Shannon Information Content 샤논 정보량 척도	하나의 사건이 일어났을 때 얻는 정보량	h​	얻는 정보량 = 처낸 정보량 = 줄어든 불확실성 양 = 구분해서 표현하기 위한 비트 수
Shannon Entropy 샤논 엔트로피 척도의 전체 평균	모든 사건에 대해 평균적으로 얻는 정보량의 기대값	H	얻는 정보량의 평균 = 모든 경우를 구분해서 기록하거나 보내기 위한 평균 비트 수
H₀ 샤논 엔트로피의 특별한 경우	사건들의 확률이 모두 동일할 때	H₀	각 사건의 확률이 동일할 때, 얻는 정보량이 최대임을 전 장에서 증명했었다. 즉 이게 바로 얻는 정보량 평균 혹은 표현하기 위한 비트수 평균의 최대 상한.

 

  

> 요약2) Lossy Compression 공부 #손실 어느정도 있음

1) 심볼 단위 -> 잘 안나오는 심볼 버리기

 

2) 블락 단위 ** -> 심볼들의 시퀀스 전체를 압축

 블락 단위로 정보를 압축했을 때, 시퀀스의 길이 N이 무한대로 가면 손실률을 감안했을 때의 필요한 비트 수 상한 평균이 엔트로피로 수렴했다. 

  즉 엔트로피는 "너네는 이거보다 잘 코딩해서 압축할 수 없어~" 와 같은 압축할 수 있는 이론적 한계를 보여주며, 이걸 Shannon’s Source Coding Theorem이라고 부른다. 

 

 N이 무한대로 가면 대부분의 셋이 티피컬 집합에 속하게 된다. 티피컬 집합이란 위 처럼 시퀀스를 압축하는데 필요한 비트 수 상한 평균이 엔트로피로 수렴하는 집합이다. 

---

• Lossless Compression # Lossy와 달리 데이터를 완벽하게 복원할 수 있음 # 여긴 심볼 코딩임 # 아직 손실 고려 X

 Lossless compression이란 심볼 하나하나를 받아서 각 심볼을 이진 문자열로 변환 즉 비트로 압축하는 방식이다. Lossy와 달리 변환 후에 다시 원본으로 돌릴 때 완벽하게 복원할 수 있어야 한다. 

example1)

위 예시를 잘 보자. 헷갈리는거 없이 잘 복원될 것이다.

 example2)

 이렇게 lossless 심볼 코딩을 했다고 하자. 이 때의 평균 비트 길이는 4가 된다. 하지만 엔트로피 즉 이 정보를 압축하기 위한 평균 비트 수를 계산하면 다음과 같이 나오게 된다.

 즉 비트 수 여백이 너무 많은 비효율적인 인코딩 방법이었다.

 

-> 자 그러면 어떻게 심볼 하나 하나를 비트 위에 인코딩하고, 원래 심볼로 디코딩하는게 최적 방법일까?

cf. 여기서의 결론도 결국 심볼 코딩의 평균 길이는 결국 엔트로피에 수렴한다는 것이다. 이걸 알아볼 것이다.

 

 

• Good Symbol Codes

 좋은 심볼 코드는 위 3개의 조건을 만족해야한다.

조건 1) 인코딩된 비트를 보고 유니크하게 복원할 수 있어야한다.

유니크하지 않으므로 좋은 코드 x

조건 2) 디코딩이 쉬워야한다 = Prefix 해야한다. 

 쉽게 말하면 인코딩된 비트를 하나 씩 앞에서부터 해석하는데, 이 때 중간 과정에서도 다른 심볼과 헷갈리면 안된다는 것이다. 유니크 조건과 헷갈릴 수 있다. 다음 예시를 보자.

 각 코드의 인코딩된 비트를 다른 비트와 비교하며 하나 씩 앞에서부터 읽어보면 이해할 수 있다. 중간 과정에서 다른 비트 구성 전체가 들어오지 않는다.

 하지만 이 예시의 경우, b 코드를 읽는 중간.. 첫 번째 인덱스의 코드를 읽는 과정부터 어? a인가? 생각할 수 있다. a의 인코딩 비트는 1이 전체적으로 다 들어왔기 때문이다. 즉 다음을 읽을 때 까지 a가 아님을 알 수가 없다.. 이런게 바로 Prefix하지 않은 것이다. 물론 끝까지 읽으면 유니크하게 디코딩은 할 수 있다.

 

조건3) 코드 길이 평균이 최대한 짧아야 한다. = 엔트로피와 같아야한다.

 엔트로피의 정의는 해당 정보의 정보량 평균 즉 표현하기 위해 압축할 수 있는 평균 비트 수였다. 이 비트 길이에 가까워야 좋은 코드가 된다. 위 예시는 좋은 코드다.

 

 3개의 조건을 전부 만족해야 좋은 코드이기 때문에, 뭐 하나만 줄이면 안된다. 아래 예시를 보자.

  길이를 줄이면서 좋은 코드가 아니게 됐다.. 

 

 하지만 하나를 줄이는 대신 하나를 늘리면 어떨까? 

  좋은 코드가 됐다. 

 

-> 편법으로 코드를 줄이려고 하면 uniquely decodable가 깨질 수 밖에 없다. 이 때 uniquely decodable를 유지하려면 결국 다른 코드의 길이는 늘려줘야한다. 이러한 균형을 수학적으로 보이는게 바로 바로 Kraft Inequality이다. 이에 대해 공부해보자.

 

 

• Kraft Inequality *정의 암기* # Uniquely decodable 더 나아가 Prefix까지 체크 가능

   손실 없이 인코딩 하므로, 모든 경우의 수 즉 모든 심볼에 대해서 코드가 존재할 것이다. 이 코드의 각 길이를 {li​}라고 하자.

이 코드 길이에 대하여 위와 같은 식을 만족하는 경우 Uniquely decodable하다. 이게 바로 Kraft Inequality이다.

 

 이를 그림으로 보면 다음과 같다.  C0, C3 전부 Uniquely decodable함을 알 수 있다.

height = 2^l

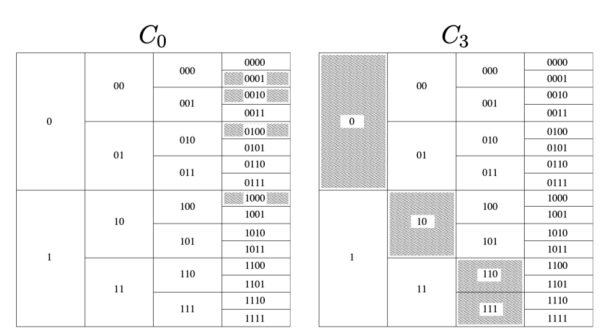
  이러한 Kraft Inequality 그림을 통해 알 수 있는 유용한 두 정보가 있다. 이를 알아두자.

1. 코드 블럭 높이의 합이 1보다 작으면 Uniquely decodable

2. 코드 블럭을 오른쪽으로 사영했을 때, 겹치지 않으면 Prefix
-> 모든 코드워드가 리프 노드에 있으면 Prefix-Free가 자동으로 만족된다. 만약 중간 노드에 존재하면 다른 코드가 그 아래로 뻗을 수 있어서 Prefix-Free가 깨진다.

 

 참고로 Kraft Inequality를 만족하면 Uniquely decodable는 무조건 만족하고, 어떻게 잘 움직여서 겹치지 않게 하면 Prefix하게도 만들 수 있다.

 

 

 두 조건을 쉽게 체크하는 방법에 대해 알아보았다. 이제 마지막 조건 코드의 평균 길이가 엔트로피에 가까워야함을 보이자.

 

• Maximum Compression # 코드의 길이는 짧아야함

 엔트로피의 정의는 해당 정보의 정보량 평균 즉 표현하기 위해 압축할 수 있는 평균 비트 수였다. 이 비트 길이에 가까워야 좋은 코드가 된다. 이를 공부해보자.

 

Q. 심볼 코드는 어디까지 짧아질 수 있을까? *** 다음과 같이 상한, 하한을 구할 수 있다.

 

 상한을 구하는 걸 Source Coding Theorem for Symbol Codes라고 부른다. 블락 단위의 시퀀스를 압축했을 때 나왔던 Shannon’s Source Coding Theorem와 다른 것임을 잘 인지하고 있어야한다. 이건 심볼 단위이다.

 

 하한을 구하는 걸 Existence of a prefix code C 라고 부른다. H$X$보다 약간 큰 수준까지 압축 가능한 prefix-free 코드가 존재한다는 뜻이다.

 

 이렇게 심볼 코드가 샤먼 엔트로피 근처까지 짧아질 수 있음을 알게 되었다. 이제 어떻게 좋은 코드를 찾을 것인가를 고민해볼 필요가 있다. 이 방법이 바로 허프만 코딩이다.

 

 

• Huffman Coding # 좋은 심볼 코드를 찾는 방법

 방법은 간단하다. 우선 모든 심볼들과 확률을 쭉 쓴다. 이후 각 스텝마다 한 번의 묶음을 진행한다. 이 때 확률이 두 개를 하나로 묶는다. 그리고 엣지에 0, 1을 할당한다. 이걸 반복해서 끝까지 오면 이제 맨 끝에서 심볼까지 가는 길은 하나다.

-> 되돌아가면서 만난 0, 1을 기록하여 이걸 코드로 쓴다.

 

 Q. 허프만 코드를 말고 더 좋은 코드는 없는가? -> 그렇다.

1) 허프만 코드는 리프 노프 노드만 쓰기에, prefix 코드이다.

2) 이진 트리에 성질에 따라 ∑2^−li​=1 를 무조건 만족하게 된다. 그림을 확인하라

3) 두 심볼 a, b가 있고 a의 코드 길이가 b보다 짧다고 생각해보자. a를 줄이면 ∑2^−li​=1 를 맞추기 위해 b의 길이를 늘려야한다. 그러면 평균 코드 길이가 길어져 더이상 최적이 아니다.